
分析 (1)由等差数列的通项公式可知:$\left\{\begin{array}{l}{4{a}_{1}+6d=14}\\{({a}_{1}+2d)^{2}={a}_{1}({a}_{1}+6d)}\end{array}\right.$,即可求得a1和d,即可求得数列{an}的通项公式;
(2)由(1)可知$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{(n+1)(n+2)}$=$\frac{1}{n+1}$-$\frac{1}{n+2}$,利用“裂项法”即可求得数列$\left\{{\frac{1}{{{a_n}{a_{n+1}}}}}\right\}$的前n项和Tn,$\frac{T_n}{n+2}$=$\frac{n}{2(n+2)^{2}}$=$\frac{1}{2(n+\frac{4}{n}+4)}$,由基本不等式的性质,即可求得$\frac{T_n}{n+2}$的最大值.
解答 解:(1)设等差数列公差为d.由已知得$\left\{\begin{array}{l}{4{a}_{1}+6d=14}\\{({a}_{1}+2d)^{2}={a}_{1}({a}_{1}+6d)}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{a}_{1}=2}\\{d=1}\end{array}\right.$或$\left\{\begin{array}{l}{d=0}\\{{a}_{1}=\frac{7}{2}}\end{array}\right.$ (舍去)
∴an=a1+(n-1)d=n+1,
数列{an}的通项公式an=n+1;
(2)由(1)可知:$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{(n+1)(n+2)}$=$\frac{1}{n+1}$-$\frac{1}{n+2}$,
∵数列$\left\{{\frac{1}{{{a_n}{a_{n+1}}}}}\right\}$的前n项和Tn,Tn=($\frac{1}{2}$-$\frac{1}{3}$)+($\frac{1}{3}$-$\frac{1}{4}$)+…+($\frac{1}{n+1}$-$\frac{1}{n+2}$),
=$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{n+1}$-$\frac{1}{n+2}$,
=$\frac{1}{2}$-$\frac{1}{n+2}$,
=$\frac{n}{2(n+2)}$
∴$\frac{T_n}{n+2}$=$\frac{n}{2(n+2)^{2}}$=$\frac{1}{2(n+\frac{4}{n}+4)}$≤$\frac{1}{2(2\sqrt{n×\frac{4}{n}}+4)}$=$\frac{1}{16}$,
当且仅当n=$\frac{4}{n}$,解得:n=2,
∴$\frac{T_n}{n+2}$的最大值$\frac{1}{16}$.
点评 本题考查等差数列的通项公式及前n项和公式,考查“裂项法”求数列的前n项,基本不等式的应用,考查数列与不等式的综合应用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 必要非充分条件 | B. | 充分非必要条件 | ||
| C. | 充要条件 | D. | 非充分非必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
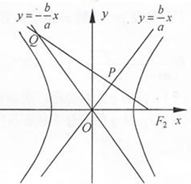 过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\;(a>0,b>0)$的右焦点F2向其一条渐近线作垂线l,垂足为P,l与另一条渐近线交于Q点,若$\overrightarrow{Q{F}_{2}}$=3$\overrightarrow{P{F}_{2}}$,则双曲线的离心率为( )
过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\;(a>0,b>0)$的右焦点F2向其一条渐近线作垂线l,垂足为P,l与另一条渐近线交于Q点,若$\overrightarrow{Q{F}_{2}}$=3$\overrightarrow{P{F}_{2}}$,则双曲线的离心率为( )| A. | 2 | B. | $\sqrt{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=$\sqrt{x}$ | B. | f(x)=lnx | C. | f(x)=($\frac{1}{2}$)x | D. | f(x)=tanx |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com