
����Ŀ��ijУ�ӲμӸ���ģ�⿼�Ե�ѧ���������ȡ60��ѧ����������ѧ�ɼ�����Ϊ�������ֳ�����[90��100����[100��110��������[140��150]��õ����²���Ƶ�ʷֲ�ֱ��ͼ���۲�ͼ�е���Ϣ���ش��������⣺ 
����ȫƵ�ʷֲ�ֱ��ͼ��
�����Ʊ��ο��Ե���ѧƽ���ɼ���ͬһ���е������ø���������е�ֵ����������
�����÷ֲ�����ķ����ڷ�����Ϊ[110��130����ѧ���ɼ��г�ȡһ������Ϊ6���������ٴ���6����������ȡ2�˳ɼ�����������1�˳ɼ��ڷ�����[120��130���ڵĸ��ʣ�
���𰸡��⣺��������[120��130���ڵ�Ƶ��1����0.1+0.15+0.15+0.25+0.05��=1��0.7=0.3�� ��˲���ij����εĸ�Ϊ0.03����ȫƵ�ʷֲ�ֱ��ͼΪ�� 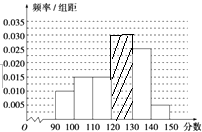
������ƽ����Ϊ ![]()
���������⣬[110��120�������ε�������[120��130�������ε�����֮��Ϊ1��2��
�÷ֲ�����ķ����ڷ�����Ϊ[110��130����ѧ���ɼ��г�ȡһ������Ϊ6��������
����[110��120���������ڳ�ȡ2�˳ɼ����ֱ��Ϊm��n��
��[120��130���������ڳ�ȡ4�˳ɼ����ֱ��Ϊa��b��c��d��
�衰��6����������ȡ2�˳ɼ���������1�˳ɼ��ڷ�����[120��130���ڡ�Ϊ�¼�A��
������¼�����{��m��n������m��a������m��b������m��c������m��d������n��a����
��n��b������n��c������n��d������a��b������a��c����
��a��d������b��c������b��d������c��d��}����15����
�¼�A�����Ļ����¼���{��m��n������m��a������m��b����
��m��c������m��d������n��a������n��b������n��c������n��d��}��9����
��P��A��= ![]() =
= ![]()
���������������������[120��130���ڵ�Ƶ�ʣ�����ij����εĸߣ��ɴ��ܲ�ȫƵ�ʷֲ�ֱ��ͼ����������Ƶ�ʷֲ�ֱ��ͼ�ܹ���ƽ���֣������÷ֲ�����ķ����ڷ�����Ϊ[110��130����ѧ���ɼ��г�ȡһ������Ϊ6������������[110��120���������ڳ�ȡ2�˳ɼ����ֱ��Ϊm��n����[120��130���������ڳ�ȡ4�˳ɼ����ֱ��Ϊa��b��c��d���ɴ������оٷ������������1�˳ɼ��ڷ�����[120��130���ڵĸ��ʣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������![]() �У���
����![]() ��
�� ![]() �ֱ�����
�ֱ�����![]() ��
�� ![]() �ϵĵ㣬��
�ϵĵ㣬��![]() ��
��

����֤����ƽ��![]() ƽ��
ƽ��![]() ��
��
������![]() ��������
��������![]() ������ֵ��
������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��l����P��1��1��������ֱ��l1��x��y+3=0��l2��2x+y��6=0�ֱ��ڵ�A��B�����߶�AB����Pƽ�֣� ��
��1��ֱ��l�ķ��̣�
��2����OΪԲ���ұ�l�صõ��ҳ�Ϊ ![]() ��Բ�ķ��̣�
��Բ�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������f��x��=sin��2x+�գ���ͼ������ƽ�� ![]() ����λ�����õ��ĺ���ͼ�����y��Գƣ���յ�һ������ȡֵΪ�� ��
����λ�����õ��ĺ���ͼ�����y��Գƣ���յ�һ������ȡֵΪ�� ��
A.![]()
B.![]()
C.0
D.- ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC��һ��O���� ![]() =
= ![]() ������ABC������Ͷһ���㣬��õ��OAC�ڵĸ���Ϊ�� ��
������ABC������Ͷһ���㣬��õ��OAC�ڵĸ���Ϊ�� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����0������ ![]() ����
���� ![]() ���£�0��cos��
���£�0��cos�� ![]() +����=
+����= ![]() ��cos��
��cos�� ![]() ��
�� ![]() ��=
��= ![]() ����cos����+
����cos����+ ![]() ��=�� ��
��=�� ��
A.![]()
B.�� ![]()
C.![]()
D.�� ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������f��x��=Asin����x+�գ���A��0���أ�0��|��|�� ![]() ����x��R���IJ���ͼ����ͼ��ʾ��
����x��R���IJ���ͼ����ͼ��ʾ��
��������f��x���Ľ���ʽ������f��x���ĵ����������䣻
��������f��x������Сֵ��ָ������f��x��ȡ��Сֵʱ��Ӧ��x��ֵ��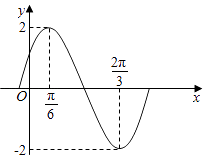
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxoy�У���֪ԲC1����x+3��2+��y��1��2=4��ԲC2����x��4��2+��y��5��2=4
��1����ֱ��l����A��4��0�����ұ�ԲC1�صõ��ҳ�Ϊ2 ![]() ����ֱ��l�ķ���
����ֱ��l�ķ���
��2����PΪƽ���ϵĵ㣬���㣺���ڹ���P�������Ի��ഹֱ��ֱ��l1��l2 �� ���Ƿֱ���ԲC1��C2�ཻ����ֱ��l1��ԲC1�صõ��ҳ���ֱ��l2��ԲC2�صõ��ҳ���ȣ����������������ĵ�P�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com