
分析 (I)利用数量积运算性质、倍角公式、和差公式可得:f(x)=$5sin(2x+\frac{π}{6})$+$\frac{7}{2}$,可得周期T,令$sin(2x+\frac{π}{6})$=0,即可解出对称中心.
(II)利用正弦函数的单调性即可得出.
解答 解:(Ⅰ)$\overrightarrow a•\overrightarrow b=5\sqrt{3}cosxsinx+2{cos^2}x,{|{\overrightarrow b}|^2}={sin^2}x+4{cos^2}x$,
f(x)=$5\sqrt{3}cosxsinx+{sin^2}x+6{cos^2}x=\frac{{5\sqrt{3}}}{2}sin2x+\frac{1-cos2x}{2}+3({1+cos2x})$
=$5(\frac{\sqrt{3}}{2}sin2x+\frac{1}{2}cos2x)$+$\frac{7}{2}$
=$5sin(2x+\frac{π}{6})$+$\frac{7}{2}$,
∴$T=\frac{2π}{2}$=π.
令$sin(2x+\frac{π}{6})$=0,解得$2x+\frac{π}{6}$=kπ,解得x=$\frac{kπ}{2}$-$\frac{π}{12}$(k∈Z).
∴f(x)的对称中心为$(\frac{kπ}{2}-\frac{π}{12},\frac{7}{2})$,(k∈Z).
(Ⅱ)解不等式$2kπ-\frac{π}{2}≤2x+\frac{π}{6}≤2kπ+\frac{π}{2}$得:$kπ-\frac{π}{3}≤x≤kπ+\frac{π}{6}$.
令k=0,∴$-\frac{π}{3}≤x≤\frac{π}{6}$,∴$0≤x≤\frac{π}{6}$,
$k=1,\frac{2π}{3}≤x≤\frac{7π}{6}$,∴$\frac{2π}{3}≤x≤π$,
∴函数f(x)在[0,π]上的单调递增区间为$[{0,\frac{π}{6}}],[{\frac{2π}{3},π}]$.
点评 本题考查了数量积运算性质、倍角公式、和差公式、三角函数的图象与性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 12人 | B. | 7人 | C. | 8人 | D. | 9人 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30.8>30.7 | B. | 0.75-0.1<0.750.1 | ||
| C. | log0.50.4>log0.50.6 | D. | lg1.6>lg1.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | x1 | $\frac{1}{3}$ | x2 | $\frac{7}{3}$ | x3 |
| Asin(ωx+ϕ)+B | 0 | $\sqrt{3}$ | 0 | -$\sqrt{3}$ | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
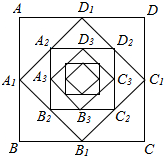 如图,正方形ABCD的边长为1,联结这个正方形各边的中点得到一个小正方形A1B1C1D1;又联结这个小正方形各边的中点得到一个更小的正方形A2B2C2D2;如此无限继续下去,设各正方形的边长依大小顺序构成数列{an}.
如图,正方形ABCD的边长为1,联结这个正方形各边的中点得到一个小正方形A1B1C1D1;又联结这个小正方形各边的中点得到一个更小的正方形A2B2C2D2;如此无限继续下去,设各正方形的边长依大小顺序构成数列{an}.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com