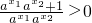Question

已知函数f（x）=a^x-a^-x，（a＞1，x∈R）．
（Ⅰ） 判断并证明函数f（x）的奇偶性；
（Ⅱ）判断并证明函数f（x）的单调性；
（Ⅲ）若f（1-t）+f（1-t²）＜0，求实数t的取值范围．

Answer 1

解：（Ⅰ）因为函数f（x）的定义域为R，又f（-x）=a^-x-a^x=-f（x）
所以f（x）是奇函数
（Ⅱ）函数f（x）为R上的增函数．
证明：在R上任取x₁＜x_2，
则=
=
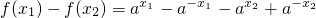
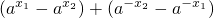
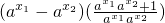
因为x₁＜x₂，又a＞1，所以，，
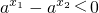
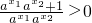
∴f（x₁）-f（x₂）＜0
所以f（x₁）＜f（x₂）．
所以函数f（x）为R上的增函数
（Ⅲ）由f（1-t）+f（1-t²）＜0，可得f（1-t）＜-f（1-t²）．
由函数f（x）是奇函数，可得f（1-t）＜f（t²-1）．
又函数f（x）为R上的增函数，所以1-t＜t²-1，即t²+t-2＞0．
解得　t＜-2，或t＞1
分析：（Ⅰ） 判断并证明函数f（x）的奇偶性；
判断奇偶性，先求定义域，看是否关于原点中心对称，若不是，则为非奇非偶函数；若是，再判断f（-x）与f（x）的关系，得出结论．
（Ⅱ）判断并证明函数f（x）的单调性；
按照定义去判断，取值，作差，变形，判断符号，得出结论．
（Ⅲ）若f（1-t）+f（1-t²）＜0，求实数t的取值范围．
先移项，得f（1-t）＜-f（1-t²），根据奇函数，f（1-t）＜f（t²-1），再根据单调性，求出t的取值范围．
点评：本题考查了函数的奇偶性的判断，函数单调性的证明，抽象函数性质应用，关键是正确应用函数的基本性质解题．
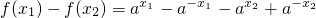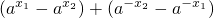
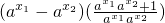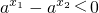