

| A. | 16 | B. | 20 | C. | 24 | D. | 18 |
分析 如图所示,连接OA,OB.过点O作OC⊥AB,垂足为C.利用垂径定理可得AC,可得cos∠OAB.利用向量的三角形法则计算即可.
解答 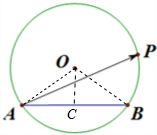 解:如图所示,连接OA,OB.过点O作OC⊥AB,垂足为C.设
解:如图所示,连接OA,OB.过点O作OC⊥AB,垂足为C.设
则AC=$\frac{1}{2}$AB=2,
∴cos∠OAB=$\frac{AC}{OA}$=$\frac{2}{3}$,
∴$\overrightarrow{AB}$•$\overrightarrow{AP}$=$\overrightarrow{AB}$•($\overrightarrow{OP}$-$\overrightarrow{OA}$)=$\overrightarrow{AB}$•$\overrightarrow{OP}$-$\overrightarrow{AB}$•$\overrightarrow{OA}$=$\overrightarrow{AB}$•$\overrightarrow{OP}$-$\overrightarrow{AB}$•$\overrightarrow{OA}$=|$\overrightarrow{AB}$|•|$\overrightarrow{OP}$|cos$<\overrightarrow{AB}$,$\overrightarrow{OP}$>+4×3cos∠OAB≤4×3×1+4×3×$\frac{2}{3}$=20,
当且仅当$\overrightarrow{OP}$∥$\overrightarrow{AB}$且同向时取等号,
∴$\overrightarrow{AB}•\overrightarrow{AP}$的最大值为20,
故选:B.,
点评 本题考查了向量的数量积运算、垂径定理、向量共线定理,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-6)∪(6,+∞) | B. | (-∞,-4)∪(4,+∞) | C. | (-∞,-2)∪(2,+∞) | D. | (-∞,-1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
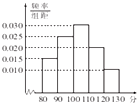 某班k名学生在一次考试中数学成绩绘制的频率分布直方图如图,若在这k名学生中,数学成绩不低于90分的人数为34,则k=( )
某班k名学生在一次考试中数学成绩绘制的频率分布直方图如图,若在这k名学生中,数学成绩不低于90分的人数为34,则k=( )| A. | 40 | B. | 46 | C. | 48 | D. | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 1 | 2 | 3 | 4 | 5 |
| y | 2 | 3 | 4 | 4 | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com