
分析 直接利用诱导公式化简取值即可.
解答 解:(1)cos(-$\frac{17π}{4}$)=cos$\frac{π}{4}$=$\frac{\sqrt{2}}{2}$;
(2)sin(-1574°)=-sin134°=-sin46°;
(3)sin(-2160°52′)=-sin0°52′;
(4)cos(-1751°36′)=cos48°8′;
(5)cos1 615°8′=-cos4°52′;
(6)sin(-$\frac{26}{3}$π)=-sin$\frac{2π}{3}$=-$\frac{\sqrt{3}}{2}$.
点评 本题考查三角函数的化简求值,基本知识的考查.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
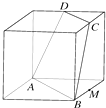
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{6}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 21 | B. | 22 | C. | 23 | D. | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1) | B. | [0,2] | C. | [-2,2) | D. | [-1,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com