
| A. | $\frac{π}{3}$ | B. | $\frac{3π}{4}$ | C. | $\frac{5π}{6}$ | D. | $\frac{2π}{3}$ |
分析 利用余弦定理,结合基本不等式,即可求出∠AFB的最大值.
解答 解:因为${x_1}+{x_2}+4=\frac{{2\sqrt{3}}}{3}|{AB}|$,|AF|+|BF|=x1+x2+4,所以$|{AF}|+|{BF}|=\frac{{2\sqrt{3}}}{3}|{AB}|$.
在△AFB中,由余弦定理得:$cos∠AFB=\frac{{{{|{AF}|}^2}+{{|{BF}|}^2}-{{|{AB}|}^2}}}{{2|{AF}|•|{BF}|}}$=$\frac{{{{(|{AF}|+|{BF}|)}^2}-2|{AF}|•|{BF}|-{{|{AB}|}^2}}}{{2|{AF}|•|{BF}|}}=\frac{{\frac{4}{3}{{|{AB}|}^2}-{{|{AB}|}^2}}}{{2|{AF}|•|{BF}|}}-1=\frac{{\frac{1}{3}{{|{AB}|}^2}}}{{2|{AF}|•|{BF}|}}-1$.
又$|{AF}|+|{BF}|=\frac{{2\sqrt{3}}}{3}|{AB}|≥2\sqrt{|{AF}|•|{BF}|}⇒|{AF}|•|{BF}|≤\frac{1}{3}{|{AB}|^2}$.
所以$cos∠AFB≥\frac{{\frac{1}{3}{{|{AB}|}^2}}}{{2×\frac{1}{3}{{|{AB}|}^2}}}-1=-\frac{1}{2}$,∴∠AFB的最大值为$\frac{2π}{3}$,
故选D.
点评 本题考查抛物线的定义,考查余弦定理、基本不等式的运用,属于中档题.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
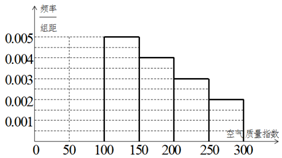 某中学环保社团参照国家环境标准,制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过300):
某中学环保社团参照国家环境标准,制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过300):| 空气质量指数 | (0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] |
| 空气质量等级 | 1级优 | 2级良 | 3级轻度污染 | 4级中度污染 | 5级重度污染 | 6级严重污染 |
| 空气质量指数 | 频数 | 频率 |
| (0,50] | x | a |
| (50,100] | y | b |
| (100,150] | 25 | 0.25 |
| (150,200] | 20 | 0.2 |
| (200,250] | 15 | 0.15 |
| (250,300] | 10 | 0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | (0,1] | C. | (0,1) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 52 | B. | $2\sqrt{13}$ | C. | 100-48$\sqrt{3}$ | D. | $\sqrt{100-48\sqrt{3}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com