Question

4．正方体ABCD-A₁B₁C₁D₁被平面B₁D₁C截去一部分后得到几何体AB₁D₁-ABCD．如图所示．
（1）在几何体AB₁D₁-ABCD的面上画出一条线段，使该线段所在的直线平行于平面B₁D₁C．
（2）设E为B₁D₁的中点，求证：B₁D₁⊥平面A₁ECA．

Answer 1

分析 （1）连接BD，则BD∥平面B₁D₁C，利用正方形的性质及线面平行的判定定理即可证明．
（2）利用等腰三角形的性质可得B₁D₁⊥A₁E，进而利用线面垂直的判定定理即可证明．

解答 解：（1）如图，连接BD，则BD∥平面B₁D₁C，
证明：∵由已知可得：BD∥B₁D₁，且BD?平面AB₁D₁，
∴BD∥平面B₁D₁C．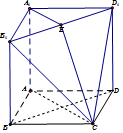

（2）证明：在等腰A₁B₁D₁中，E为B₁D₁的中点，
所以，B₁D₁⊥A₁E，
由已知可得：AA₁⊥平面A₁B₁D₁，
所以，AA₁⊥B₁D₁，
所以，B₁D₁⊥平面A₁ECA．

点评 本题主要考查了线面平行的判定定理，等腰三角形的性质，线面垂直的判定定理的应用，考查了数形结合思想，属于中档题．