
设f(x)=-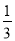 x3+
x3+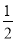 x2+2ax,若f(x)在(
x2+2ax,若f(x)在(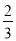 ,+∞)上存在单调递增区间,则实数a的取值范围为( )
,+∞)上存在单调递增区间,则实数a的取值范围为( )
A.a>-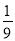 B.a<-
B.a<-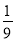 C.a>
C.a> D.不存在
D.不存在
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-3函数的奇偶性与周期性(解析版) 题型:填空题
已知函数f(x)=x3+3x对任意的m∈[-2,2],f(mx-2)+f(x)<0恒成立,则x的取值范围为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-1函数的概念、定义域和值域(解析版) 题型:选择题
如图,是张大爷晨练时所走的离家距离(y)与行走时间(x)之间的函数关系的图象.若用黑点表示张大爷家的位置,则张大爷散步行走的路线可能是( )


查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-12导数的应用二(解析版) 题型:选择题
函数f(x)=x2-2ax+a在区间(-∞,1)上有最小值,则函数g(x)= 在区间(1,+∞)上一定( )
在区间(1,+∞)上一定( )
A.有最小值 B.有最大值 C.是减函数 D.是增函数
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-11导数的应用一(解析版) 题型:解答题
设f(x)=ln(1+x)-x-ax2.
(1)当x=1时,f(x)取到极值,求a的值;
(2)当a满足什么条件时,f(x)在区间[-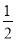 ,-
,-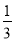 ]上有单调递增区间?
]上有单调递增区间?
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-10导数的概念及运算(解析版) 题型:解答题
已知函数f(x)=x3+x-16.
(1)求曲线y=f(x)在点(2,-6)处的切线的方程;
(2)直线l为曲线y=f(x)的切线,且经过原点,求直线l的方程及切点坐标;
(3)如果曲线y=f(x)的某一切线与直线y=- x+3垂直,求切点坐标与切线的方程.
x+3垂直,求切点坐标与切线的方程.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-10导数的概念及运算(解析版) 题型:填空题
已知函数f(x)=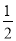 x-
x-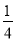 sinx-
sinx-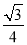 cosx的图象在点A(x0,y0)处的切线斜率为1,则tanx0=________.
cosx的图象在点A(x0,y0)处的切线斜率为1,则tanx0=________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-8n次独立重复实验与二项分布(解析版) 题型:选择题
在高三的一个班中,有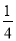 的学生数学成绩优秀,若从班中随机找出5名学生,那么数学成绩优秀的学生数ξ~B(5,
的学生数学成绩优秀,若从班中随机找出5名学生,那么数学成绩优秀的学生数ξ~B(5,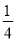 ),则P(ξ=k)取最大值的k值为( )
),则P(ξ=k)取最大值的k值为( )
A.0 B.1 C.2 D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com