
设f(x)=ln(1+x)-x-ax2.
(1)当x=1时,f(x)取到极值,求a的值;
(2)当a满足什么条件时,f(x)在区间[-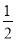 ,-
,-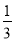 ]上有单调递增区间?
]上有单调递增区间?
(1)a=-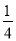 (2)a∈(-1,+∞).
(2)a∈(-1,+∞).
【解析】【解析】
(1)由题意知,f(x)的定义域为(-1,+∞),
且f′(x)=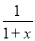 -2ax-1=
-2ax-1=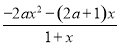 ,
,
由题意得:f′(1)=0,则-2a-2a-1=0,得a=-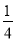 ,
,
又当a=-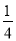 时,f′(x)=
时,f′(x)=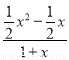 =
=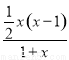 ,
,
当0<x<1时,f′(x)<0;当x>1时,f′(x)>0,
所以f(1)是函数f(x)的极大值,所以a=-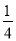 .
.
(2)要使f(x)在区间[-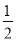 ,-
,-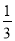 ]上有单调递增区间,
]上有单调递增区间,
即要求f′(x)>0在区间[-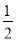 ,-
,-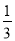 ]上有解,
]上有解,
当-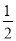 ≤x≤-
≤x≤-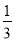 时,
时,
f′(x)>0等价于2ax+(2a+1)>0.
①当a=0时,不等式恒成立;
②当a>0时,得x>-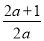 ,
,
此时只要-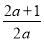 <-
<-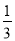 ,
,
解得a>0;
③当a<0时,得x<-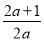 ,
,
此时只要- >-
>-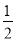 ,
,
解得-1<a<0.
综上所述,a∈(-1,+∞).


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-4二次函数与幂函数(解析版) 题型:选择题
若函数f(x)=x2-ax-a在区间[0,2]上的最大值为1,则实数a等于( )
A.-1 B.1 C.2 D.-2
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-1函数的概念、定义域和值域(解析版) 题型:解答题
已知函数f(x)=x2-4ax+2a+6,x∈R.
(1)若函数的值域为[0,+∞),求a的值;
(2)若函数的值域为非负数集,求函数f(a)=2-a|a+3|的值域.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-12导数的应用二(解析版) 题型:填空题
函数f(x)=-x3+mx2+1(m≠0)在(0,2)内的极大值为最大值,则m的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-11导数的应用一(解析版) 题型:解答题
已知函数f(x)=xlnx-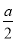 x2.
x2.
(1)当a=1时,函数y=f(x)有几个极值点?
(2)是否存在实数a,使函数f(x)=xlnx-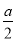 x2有两个极值?若存在,求实数a的取值范围;若不存在,请说明理由.
x2有两个极值?若存在,求实数a的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-11导数的应用一(解析版) 题型:选择题
设f(x)=-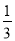 x3+
x3+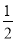 x2+2ax,若f(x)在(
x2+2ax,若f(x)在(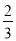 ,+∞)上存在单调递增区间,则实数a的取值范围为( )
,+∞)上存在单调递增区间,则实数a的取值范围为( )
A.a>-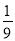 B.a<-
B.a<-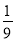 C.a>
C.a> D.不存在
D.不存在
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-10导数的概念及运算(解析版) 题型:填空题
记定义在R上的函数y=f(x)的导函数为f′(x).如果存在x0∈[a,b],使得f(b)-f(a)=f′(x0)(b-a)成立,则称x0为函数f(x)在区间[a,b]上的“中值点”.那么函数f(x)=x3-3x在区间[-2,2]上“中值点”的个数为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-8n次独立重复实验与二项分布(解析版) 题型:解答题
深圳市某校中学生篮球队假期集训,集训前共有6个篮球,其中3个是新球(即没有用过的球),3个是旧球(即至少用过一次的球).每次训练,都从中任意取出2个球,用完后放回.
(1)设第一次训练时取到的新球个数为ξ,求ξ的分布列和数学期望;
(2)求第二次训练时恰好取到一个新球的概率.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-5古典概型(解析版) 题型:解答题
某停车场临时停车按时段收费,收费标准为:每辆汽车一次停车不超过1小时收费6元,超过1小时的部分每小时收费8元(不足1小时的部分按1小时计算).现有甲、乙二人在该停车场临时停车,两人停车都不超过4小时.
(1)若甲停车1小时以上且不超过2小时的概率为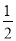 ,停车付费多于14元的概率为
,停车付费多于14元的概率为 ,求甲临时停车付费恰为6元的概率;
,求甲临时停车付费恰为6元的概率;
(2)若每人停车的时间在每个时段的可能性相同,求甲、乙二人停车付费之和为36元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com