
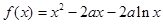 ,
,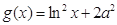 ,其中
,其中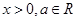 .
.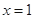 是函数
是函数 的极值点,求
的极值点,求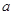 的值;
的值; 在区间
在区间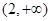 上单调递增,求
上单调递增,求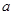 的取值范围;
的取值范围;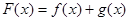 ,求证:
,求证: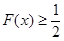 .
.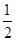 ;(2)
;(2)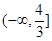 ;(3)参考解析
;(3)参考解析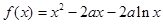 ,所以可得
,所以可得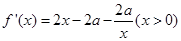 ,又
,又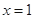 是函数
是函数 的极值点,即
的极值点,即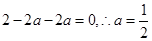 .
. 在区间
在区间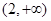 上单调递增,所以对函数
上单调递增,所以对函数 求导,然后把变量
求导,然后把变量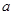 分离,求函数
分离,求函数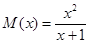 的最值即可.
的最值即可.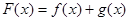 即可得到,
即可得到,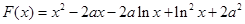 ,按
,按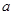 的降幂写成二次三项的形式,然后再配方,即可得到
的降幂写成二次三项的形式,然后再配方,即可得到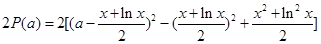 .再用放缩法即可得到结论.
.再用放缩法即可得到结论.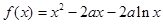 ,
,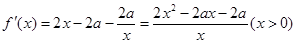 ,
,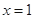 是函数
是函数 的极值点,
的极值点,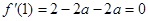 ,解得
,解得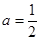 ,经检验
,经检验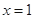 为函数
为函数 的极值点,所以
的极值点,所以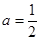 .
. 在区间
在区间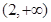 上单调递增,
上单调递增,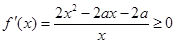 在区间
在区间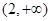 上恒成立,
上恒成立,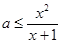 对区间
对区间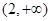 恒成立,
恒成立, 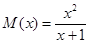 ,则
,则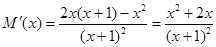
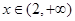 时,
时,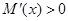 ,有
,有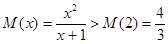 ,
, 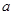 的取值范围为
的取值范围为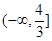 .
.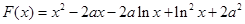
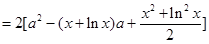 ,令
,令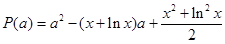 ,
,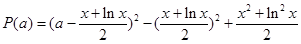
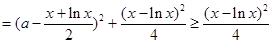
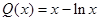 ,则
,则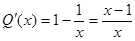 ,
,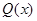 在
在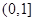 上单调递减,在
上单调递减,在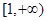 上单调递增,
上单调递增,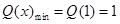 ,则
,则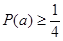 ,
,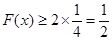 .
.
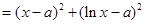
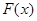 表示
表示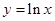 上一点
上一点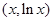 与直线
与直线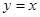 上一点
上一点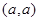 距离的平方.
距离的平方.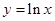 得
得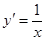 ,让
,让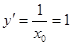 ,解得
,解得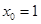 ,
, 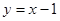 与
与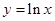 的图象相切于点
的图象相切于点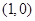 ,
,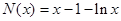 ,则
,则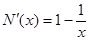 ,
,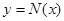 在
在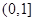 上单调递减,在
上单调递减,在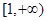 上单调递增,
上单调递增,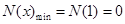 ,则
,则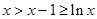 ,
,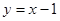 与
与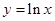 的图象相切于点
的图象相切于点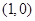 ),
),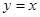 的距离为
的距离为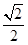 ,
,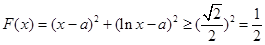 .
.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源:不详 题型:解答题
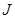 型卡车将某种水果运送(满载)到相距400km的水果批发市场.据测算,
型卡车将某种水果运送(满载)到相距400km的水果批发市场.据测算,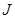 型卡车满载行驶时,每100km所消耗的燃油量
型卡车满载行驶时,每100km所消耗的燃油量 (单位:
(单位: )与速度
)与速度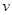 (单位:km/h)的关系近似地满足
(单位:km/h)的关系近似地满足 ,除燃油费外,人工工资、车损等其他费用平均每小时300元.已知燃油价格为7.5元/L.
,除燃油费外,人工工资、车损等其他费用平均每小时300元.已知燃油价格为7.5元/L.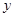 (元)(不计返程费用),将
(元)(不计返程费用),将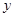 表示成速度
表示成速度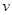 的函数关系式;
的函数关系式;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com