
分析 直接利用抛物线的性质结合已知求得(1)(2)的标准方程;设出抛物线方程y2=2px(p>0)或x2=2py(p>0),把点的坐标代入求得p,则(3)的方程可求.
解答 解:(1)∵抛物线的焦点坐标为(-2,0),∴$\frac{p}{2}=2$,则p=4,故抛物线方程为y2=-8x;
(2)∵抛物线准线方程为y=-1,∴$\frac{p}{2}=1$,则p=2,故抛物线方程为x2=4y;
(3)∵抛物线过点(1,2),∴可设抛物线方程为y2=2px(p>0)或x2=2py(p>0),
把点(1,2)代入y2=2px,得p=2,故抛物线方程为y2=4x;
代入x2=2py,得p=$\frac{1}{4}$,故抛物线方程为${x}^{2}=\frac{1}{2}y$.
∴所求抛物线方程为y2=4x或${x}^{2}=\frac{1}{2}y$.
点评 本题考查抛物线的标准方程,考查了抛物线的简单性质,是基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | -2015 | B. | 2015 | C. | 0 | D. | 2014 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
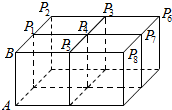 如图,四个完全相同的长方体排成一个直四棱柱:每个长方体底面为边长1的正方形,侧棱AB长为2,Pi(i=1,2…)是上底面上其余的八个点,则$\overrightarrow{AB}$•$\overrightarrow{A{P}_{i}}$(i=1,2,…)的不同值的个数为( )
如图,四个完全相同的长方体排成一个直四棱柱:每个长方体底面为边长1的正方形,侧棱AB长为2,Pi(i=1,2…)是上底面上其余的八个点,则$\overrightarrow{AB}$•$\overrightarrow{A{P}_{i}}$(i=1,2,…)的不同值的个数为( )| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com