Question

6．在△ABC中，∠BAC=90°，BC=5，D，E为边BC上的两点，且满足：$\overrightarrow{BD}=\frac{1}{3}\overrightarrow{BC}，\overrightarrow{CE}=\frac{1}{3}\overrightarrow{CB}$，则$\overrightarrow{AD}•\overrightarrow{AE}$的值为$\frac{50}{9}$．

Answer 1

分析 通过建立坐标系，设出B，C坐标，求解D、E坐标，然后向量得到数量积．

解答 解：如图：以A为原点，AB为x轴，AC为：y轴，
设B（3m，0），C（0，3n），9m²+9n²=25，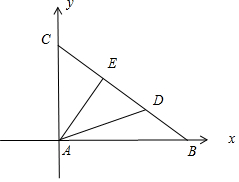
$\overrightarrow{BD}=\frac{1}{3}\overrightarrow{BC}，\overrightarrow{CE}=\frac{1}{3}\overrightarrow{CB}$，
则D（2m，n），E（m，2n），
则$\overrightarrow{AD}•\overrightarrow{AE}$=2m²+2n²=2（m²+n²）=2×$\frac{25}{9}$=$\frac{50}{9}$
故答案为：$\frac{50}{9}$

点评 本题考查向量的数量积的应用，向量在几何中的应用，考查计算能力．