
【题目】已知![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 上的点,且
上的点,且![]() ,
,![]() .
.
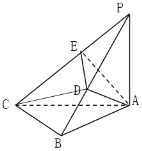
(1)求证:![]() ;
;
(2)若![]() ,直线
,直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)先证明BC⊥平面PAB,可得BC⊥AD,证明AD⊥平面PBC,得PC⊥AD,再证明PC⊥平面ADE,即可证明PC⊥DE;
(2)过点B作BE∥AP,则BZ⊥平面ABC,分别以BA,BC,BZ所在直线为x轴,y轴,z轴建立空间直角坐标系,设![]() ,根据PC⊥平面ADE,可得
,根据PC⊥平面ADE,可得![]() 是平面ADE的一个法向量,从而向量
是平面ADE的一个法向量,从而向量![]() 与
与![]() 所成的角的余弦值的绝对值为
所成的角的余弦值的绝对值为![]() ,可求PA的值,利用题目条件求出平面
,可求PA的值,利用题目条件求出平面![]() 的一个法向量,利用夹角公式可得二面角
的一个法向量,利用夹角公式可得二面角![]() 的余弦值.
的余弦值.
(1)证明:因为![]()
![]() 平面
平面![]() ,∴
,∴![]() ,
,
又![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,∴
,∴![]() .
.
又![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,∴
,∴![]() .
.
又![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,∴
,∴![]() .
.
(2)过点![]() 作
作![]() ,则
,则![]() 平面
平面![]() ,如图所示
,如图所示
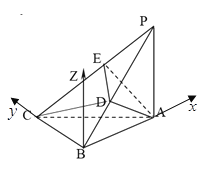
分别以![]() ,
,![]() ,
,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系.
轴建立空间直角坐标系.
设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
因为![]() 平面
平面![]() ,
,
∴![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
∴向量![]() 与
与![]() 所成的角的余弦值的绝对值为
所成的角的余弦值的绝对值为![]() ,
,
又![]() ,
,
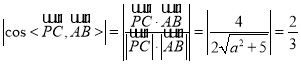 ,
,
∴![]() ,∴
,∴![]() .
.
在![]() 中,
中,![]() ,又
,又![]() ,
,
∴![]() 为
为![]() 中点,∴
中点,∴![]() ,
,
∴![]() ,
,![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则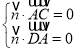 ,∴
,∴![]() ,∴
,∴![]() ,
,
又![]() 是平面
是平面![]() 的法向量,
的法向量,
∴![]() ,
,![]() ,
,
二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】我国著名的数学家秦九韶在《数书九章》提出了“三斜求积术”.他把三角形的三条边分别称为小斜、中斜和大斜.三斜求积术就是用小斜平方加上大斜平方,送到中斜平方,取相减后余数的一半,自乘而得一个数,小斜平方乘以大斜平方,送到上面得到的那个数,相减后余数被4除,所得的数作为“实”,1作为“隅”,开平方后即得面积.所谓“实”、“隅”指的是在方程![]() 中,p为“隅”,q为“实”.即若
中,p为“隅”,q为“实”.即若![]() 的大斜、中斜、小斜分别为a,b,c,则
的大斜、中斜、小斜分别为a,b,c,则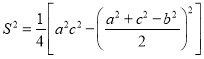 .已知点D是
.已知点D是![]() 边AB上一点,
边AB上一点,![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() 的面积为________.
的面积为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的直角顶点
的直角顶点![]() 在
在![]() 轴上,点
轴上,点![]() 为斜边
为斜边![]() 的中点,且
的中点,且![]() 平行于
平行于![]() 轴.
轴.
(Ⅰ)求点![]() 的轨迹方程;
的轨迹方程;
(Ⅱ)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,直线
,直线![]() 与
与![]() 的另一个交点为
的另一个交点为![]() .以
.以![]() 为直径的圆交
为直径的圆交![]() 轴于
轴于![]() 即此圆的圆心为
即此圆的圆心为![]() ,
,![]() 求
求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古人云:“腹有诗书气自华.”为响应全民阅读,建设书香中国,校园读书活动的热潮正在兴起.某校为统计学生一周课外读书的时间,从全校学生中随机抽取![]() 名学生进行问卷调査,统计了他们一周课外读书时间(单位:
名学生进行问卷调査,统计了他们一周课外读书时间(单位:![]() )的数据如下:
)的数据如下:
一周课外读书时间/ |
|
|
|
|
|
|
|
|
| 合计 |
频数 | 4 | 6 | 10 | 12 | 14 | 24 |
| 46 | 34 |
|
频率 | 0.02 | 0.03 | 0.05 | 0.06 | 0.07 | 0.12 | 0.25 |
| 0.17 | 1 |
(1)根据表格中提供的数据,求![]() ,
,![]() ,
,![]() 的值并估算一周课外读书时间的中位数.
的值并估算一周课外读书时间的中位数.
(2)如果读书时间按![]() ,
,![]() ,
,![]() 分组,用分层抽样的方法从
分组,用分层抽样的方法从![]() 名学生中抽取20人.
名学生中抽取20人.
①求每层应抽取的人数;
②若从![]() ,
,![]() 中抽出的学生中再随机选取2人,求这2人不在同一层的概率.
中抽出的学生中再随机选取2人,求这2人不在同一层的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为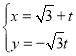 (t为参数),以坐标原点为极点,x轴正半轴为极轴,建立极坐标系,已知曲线C的极坐标方程为
(t为参数),以坐标原点为极点,x轴正半轴为极轴,建立极坐标系,已知曲线C的极坐标方程为![]() .
.
(1)求直线l的普通方程与曲线C的直角坐标方程;
(2)设点![]() ,直线l与曲线C交于不同的两点A、B,求
,直线l与曲线C交于不同的两点A、B,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com