
����Ŀ�������ƣ�������ʫ�����Ի�.��Ϊ��Ӧȫ���Ķ������������й���У�������ȳ���������.ijУΪͳ��ѧ��һ�ܿ�������ʱ�䣬��ȫУѧ���������ȡ![]() ��ѧ�������ʾ����ˣ�ͳ��������һ�ܿ������ʱ�䣨��λ��
��ѧ�������ʾ����ˣ�ͳ��������һ�ܿ������ʱ�䣨��λ��![]() �����������£�
�����������£�
һ�ܿ������ʱ��/ |
|
|
|
|
|
|
|
|
| �ϼ� |
Ƶ�� | 4 | 6 | 10 | 12 | 14 | 24 |
| 46 | 34 |
|
Ƶ�� | 0.02 | 0.03 | 0.05 | 0.06 | 0.07 | 0.12 | 0.25 |
| 0.17 | 1 |
��1�����ݱ������ṩ�����ݣ���![]() ��
��![]() ��
��![]() ��ֵ������һ�ܿ������ʱ�����λ��.
��ֵ������һ�ܿ������ʱ�����λ��.
��2���������ʱ�䰴![]() ��
��![]() ��
��![]() ���飬�÷ֲ�����ķ�����
���飬�÷ֲ�����ķ�����![]() ��ѧ���г�ȡ20��.
��ѧ���г�ȡ20��.
����ÿ��Ӧ��ȡ��������
������![]() ��
��![]() �г����ѧ���������ѡȡ2�ˣ�����2�˲���ͬһ��ĸ���.
�г����ѧ���������ѡȡ2�ˣ�����2�˲���ͬһ��ĸ���.
���𰸡���1��![]() ��
��![]() ��
��![]() �����
����λ��![]() ����2���������г�ȡ�������ֱ�Ϊ2��5��13����
����2���������г�ȡ�������ֱ�Ϊ2��5��13����![]()
��������
��1������Ƶ�ʷֲ�ֱ���������ʣ��������![]() ���õ�
���õ�![]() ��
��![]() ���ٽ����λ���ļ��㷽�����������.
���ٽ����λ���ļ��㷽�����������.
��2����������֪�÷ֲ�����ķ����������г�ȡ20�ˣ����ݳ����ȣ�����������г�ȡ��������
���ɢ�֪����![]() �ڱ���ȡ��ѧ���ֱ�Ϊ
�ڱ���ȡ��ѧ���ֱ�Ϊ![]() ��
��![]() �ڱ���ȡ��ѧ���ֱ�Ϊ
�ڱ���ȡ��ѧ���ֱ�Ϊ![]() �������оٷ��õ������¼������������ùŵ���͵ĸ��ʼ��㹫ʽ���������.
�������оٷ��õ������¼������������ùŵ���͵ĸ��ʼ��㹫ʽ���������.
��1�������⣬�ɵ�![]() ������
������![]() ��
��![]() .
.
��һ�ܿ������ʱ�����λ��Ϊ![]() Сʱ��
Сʱ��
��![]() �����
�����![]() ��
��
��һ�ܿ������ʱ�����λ��ԼΪ![]() Сʱ.
Сʱ.
��2����������֪�÷ֲ�����ķ����������г�ȡ20�ˣ�������Ϊ![]() ��
��
����Ϊ![]() ��
��![]() ��
��![]() ��Ƶ���ֱ�Ϊ20��50��130��
��Ƶ���ֱ�Ϊ20��50��130��
���Դ�![]() ��
��![]() ��
��![]() �����г�ȡ�������ֱ�Ϊ2��5��13.
�����г�ȡ�������ֱ�Ϊ2��5��13.
���ɢ�֪����![]() ��
��![]() �����й���ȡ7�ˣ���
�����й���ȡ7�ˣ���![]() �ڱ���ȡ��ѧ���ֱ�Ϊ
�ڱ���ȡ��ѧ���ֱ�Ϊ![]() ��
��![]() �ڱ���ȡ��ѧ���ֱ�Ϊ
�ڱ���ȡ��ѧ���ֱ�Ϊ![]() ��
��
������7���������ȡ2�ˣ����������Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ������21�֣�
������21�֣�
����2�˲���ͬһ������Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ������10��.
������10��.
���¼�![]() Ϊ����2�˲���ͬһ������
Ϊ����2�˲���ͬһ������
�ɹŵ���͵ĸ��ʼ��㹫ʽ���ɵø���Ϊ![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
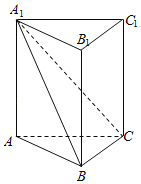
����Ŀ�����ҹ��Ŵ���ѧ�����������������н�����Ϊֱ�������Σ��Ҳ��ⴹֱ�ڵ������������֮Ϊǵ�£���ͼ����ǵ��ABC��A1B1C1�У�AB��BC��AA1��AB��ǵ�µĶ���C1��ֱ��A1C�ľ���Ϊm��C1��ƽ��A1BC�ľ���Ϊn����![]() ��ȡֵ��Χ�ǣ� ��
��ȡֵ��Χ�ǣ� ��
A.��1��![]() ��B.��
��B.��![]() ��
��![]() ��C.��
��C.��![]() ��
��![]() ��D.��
��D.��![]() ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ��ҵ���Ӹ�У2018���ҵ�����Ѿ�ҵ�Ĵ�ѧ�������������ȡ100�˽����ʾ����飬������һ�������ǵ���н���.�����鷢�֣����ǵ���н��3000Ԫ��10000Ԫ֮�䣬����ͳ�����ݵõ�����Ƶ�ʷֲ�ֱ��ͼ��
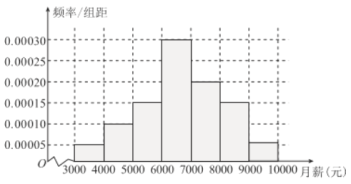
����н������![]() ����࣬����Ϊ�ô�ѧ������������ҵ����������ѧ����ѧУ����ϵ���ˣ���ѯ��н���͵�ԭ�Ӷ�Ϊ��������ҵ�ṩ���õ�ָ�����.����
����࣬����Ϊ�ô�ѧ������������ҵ����������ѧ����ѧУ����ϵ���ˣ���ѯ��н���͵�ԭ�Ӷ�Ϊ��������ҵ�ṩ���õ�ָ�����.����![]() ��
��![]() �ֱ�Ϊ����ƽ��������������ƣ�����ɵ�
�ֱ�Ϊ����ƽ��������������ƣ�����ɵ�![]() Ԫ��ͬһ���е������ø�������е�ֵ������.
Ԫ��ͬһ���е������ø�������е�ֵ������.
��1���ָ�У2018���ѧ��������ҵ����������нΪ3600Ԫ�����ж������Ƿ���������ҵ����������ѧ����
��2��Ϊ��лͬѧ�Ƕ�������鹤����֧�֣���У���÷ֲ�����ķ�����������ǰ3���г�ȡ6�ˣ�������һ����Ʒ��������6�����ٳ�ȡ2�ˣ�������ij�������ֻ�1��������������ֻ���2����ǡ��1����н������5000 Ԫ�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ƽ��
ƽ��![]() ��
��![]() ��
��![]() ��
��![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ��
��![]() �ϵĵ㣬��
�ϵĵ㣬��![]() ��
��![]() .
.
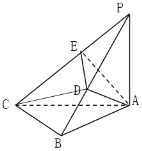
��1����֤��![]() ��
��
��2����![]() ��ֱ��
��ֱ��![]() ��ƽ��
��ƽ��![]() ���ɽǵ�����ֵΪ
���ɽǵ�����ֵΪ![]() ��������
��������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��
��![]() ��������Ϊ
��������Ϊ![]() ������������
������������![]() ����
����![]() ��
��![]() ���㣬
���㣬![]() ��
��![]() Ϊ����ԭ�㣩�����Ϊ
Ϊ����ԭ�㣩�����Ϊ![]() ��
��
��1������Բ![]() �ķ��̣�
�ķ��̣�
��2����ͼ����![]() Ϊ��Բ��һ���㣨�dz���˵㣩
Ϊ��Բ��һ���㣨�dz���˵㣩![]() ��
��![]() Ϊ���ҽ��㣬
Ϊ���ҽ��㣬![]() ���ӳ�������Բ����
���ӳ�������Բ����![]() �㣬
�㣬![]() ���ӳ�������Բ����
���ӳ�������Բ����![]() �㣬��
�㣬��![]() ��������ֵ��
��������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��
��1����![]() ������
������![]() �ĵ������䣻
�ĵ������䣻
��2����![]() ���������ʵ��
���������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019�꣬���ϵ�8ʡ�����˸߿��ĸ��ۺϷ�������ȡ��![]() ��ģʽ�������ġ���ѧ��Ӣ��ؿ���Ȼ����������������ʷ��ѡ��1�ţ�����˼�����Ρ���������ѧ��������ѡ��2��Ϊ�˸��ý������Ĺ滮����ͬѧ�Ը�һһ�������ߴο��Գɼ�����ͳ�Ʒ�����������������ʷ�ɼ��ľ�Ҷͼ��ͼ��ʾ.
��ģʽ�������ġ���ѧ��Ӣ��ؿ���Ȼ����������������ʷ��ѡ��1�ţ�����˼�����Ρ���������ѧ��������ѡ��2��Ϊ�˸��ý������Ĺ滮����ͬѧ�Ը�һһ�������ߴο��Գɼ�����ͳ�Ʒ�����������������ʷ�ɼ��ľ�Ҷͼ��ͼ��ʾ.
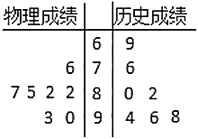
��1������ͬѧ���ѡ��3�Ź��Σ�����ѡ���������������Ź��εĸ��ʣ�
��2���Ը��ݾ�Ҷͼ������ͬѧ����������ʷ��һѧ�Ƴɼ����ȶ�.��������㣩
��3����ͬѧ���֣����������Գɼ�![]() ���֣���༶ƽ����
���֣���༶ƽ����![]() ���֣�����������ع�ϵ��ͳ���������±���ʾ�����༶ƽ����Ϊ50��ʱ�����������Գɼ�.������
���֣�����������ع�ϵ��ͳ���������±���ʾ�����༶ƽ����Ϊ50��ʱ�����������Գɼ�.������![]() ��
��![]() ʱ��ȷ��0.01��
ʱ��ȷ��0.01��
| 57 | 61 | 65 | 72 | 74 | 77 | 84 |
| 76 | 82 | 82 | 85 | 87 | 90 | 93 |
�ο����ݣ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() .
.
�ο���ʽ��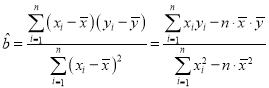 ��
��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У�����
�У�����![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ��
��![]() Ϊ������.������ԭ��
Ϊ������.������ԭ��![]() Ϊ���㣬
Ϊ���㣬![]() ��������Ϊ���Ὠ��������ϵ��ֱ��
��������Ϊ���Ὠ��������ϵ��ֱ��![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() .
.
��1��������![]() ����ͨ���̺�ֱ��
����ͨ���̺�ֱ��![]() ��ֱ�����귽�̣�
��ֱ�����귽�̣�
��2�����![]() ����ֱ��
����ֱ��![]() ������
������![]() �ཻ��
�ཻ��![]() ��
��![]() ���㣬��
���㣬��![]() ��ֵ
��ֵ
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com