
【题目】在锐角![]() 中,角
中,角![]() 的对边分别为
的对边分别为![]() ,
,![]() .
.
(1)求角![]() 的大小;
的大小;
(2)若![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1) ![]() ; (2)
; (2) ![]() .
.
【解析】
(1)利用两角和差的正弦公式进行化简即可,求角A的大小;
(2)先求得 B+C=![]() ,根据B、C都是锐角求出B的范围,由正弦定理得到b=2sinB,c=2sinC,根据 b2+c2=4+2sin(2B﹣
,根据B、C都是锐角求出B的范围,由正弦定理得到b=2sinB,c=2sinC,根据 b2+c2=4+2sin(2B﹣![]() ) 及B的范围,得
) 及B的范围,得 ![]() <sin(2B﹣
<sin(2B﹣![]() )≤1,从而得到b2+c2的范围.
)≤1,从而得到b2+c2的范围.
(1)由![]() =
=![]()
得sinAcosB+sinAcosC=cosAsinB+cosAsinC,
即sin(A﹣B)=sin(C﹣A),
则A﹣B = C﹣A,即2A=C+B,
即A=![]() ..
..
(2)当a=![]() 时,∵B+C=
时,∵B+C=![]() ,∴C=
,∴C=![]() ﹣B.由题意得
﹣B.由题意得 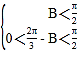 ,
,
∴![]() <B<
<B<![]() .由
.由 ![]() =2,得 b=2sinB,c=2sinC,
=2,得 b=2sinB,c=2sinC,
∴b2+c2=4 (sin2B+sin2C)=4+2sin(2B﹣![]() ).
).
∵![]() <B<
<B<![]() ,∴
,∴![]() <sin(2B﹣
<sin(2B﹣![]() )≤1,∴1≤2sin(2B﹣
)≤1,∴1≤2sin(2B﹣![]() )≤2.
)≤2.
∴5<b2+c2≤6.
故![]() 的取值范围是
的取值范围是![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】古人云:“腹有诗书气自华.”为响应全民阅读,建设书香中国,校园读书活动的热潮正在兴起.某校为统计学生一周课外读书的时间,从全校学生中随机抽取![]() 名学生进行问卷调査,统计了他们一周课外读书时间(单位:
名学生进行问卷调査,统计了他们一周课外读书时间(单位:![]() )的数据如下:
)的数据如下:
一周课外读书时间/ |
|
|
|
|
|
|
|
|
| 合计 |
频数 | 4 | 6 | 10 | 12 | 14 | 24 |
| 46 | 34 |
|
频率 | 0.02 | 0.03 | 0.05 | 0.06 | 0.07 | 0.12 | 0.25 |
| 0.17 | 1 |
(1)根据表格中提供的数据,求![]() ,
,![]() ,
,![]() 的值并估算一周课外读书时间的中位数.
的值并估算一周课外读书时间的中位数.
(2)如果读书时间按![]() ,
,![]() ,
,![]() 分组,用分层抽样的方法从
分组,用分层抽样的方法从![]() 名学生中抽取20人.
名学生中抽取20人.
①求每层应抽取的人数;
②若从![]() ,
,![]() 中抽出的学生中再随机选取2人,求这2人不在同一层的概率.
中抽出的学生中再随机选取2人,求这2人不在同一层的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为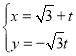 (t为参数),以坐标原点为极点,x轴正半轴为极轴,建立极坐标系,已知曲线C的极坐标方程为
(t为参数),以坐标原点为极点,x轴正半轴为极轴,建立极坐标系,已知曲线C的极坐标方程为![]() .
.
(1)求直线l的普通方程与曲线C的直角坐标方程;
(2)设点![]() ,直线l与曲线C交于不同的两点A、B,求
,直线l与曲线C交于不同的两点A、B,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程:在平面直角坐标系![]() 中,曲线
中,曲线![]() :
:![]() (
(![]() 为参数),在以平面直角坐标系的原点为极点、
为参数),在以平面直角坐标系的原点为极点、![]() 轴的正半轴为极轴,且与平面直角坐标系
轴的正半轴为极轴,且与平面直角坐标系![]() 取相同单位长度的极坐标系中,曲线
取相同单位长度的极坐标系中,曲线![]() :
:![]() .
.
(1)求曲线![]() 的普通方程以及曲线
的普通方程以及曲线![]() 的平面直角坐标方程;
的平面直角坐标方程;
(2)若曲线![]() 上恰好存在三个不同的点到曲线
上恰好存在三个不同的点到曲线![]() 的距离相等,求这三个点的极坐标.
的距离相等,求这三个点的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x),f′(x)是其导函数且满足f(x)+f′(x)>2,f(1)=2![]() ,则不等式exf(x)>4+2ex的解集为_____
,则不等式exf(x)>4+2ex的解集为_____
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列![]() 满足:
满足:![]() ,
,![]() ,其中
,其中![]() .
.
(1)若![]() ,求数列
,求数列![]() 的前
的前![]() 项的和;
项的和;
(2)若![]() ,
,![]() .
.
①求数列![]() 的通项公式;
的通项公式;
②记数列![]() 的前
的前![]() 项的和为
项的和为![]() ,若无穷项等比数列
,若无穷项等比数列![]() 始终满足
始终满足![]() ,求数列
,求数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com