
【题目】如图,圆F:![]() 和抛物线
和抛物线![]() ,过F的直线与抛物线和圆依次交于A、B、C、D四点,求
,过F的直线与抛物线和圆依次交于A、B、C、D四点,求![]() 的值是( )
的值是( )
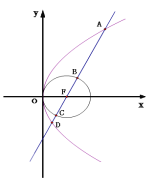
A.1B.2C.3D.无法确定
【答案】A
【解析】
可分两类讨论,若直线的斜率不存在,则直线方程为x=1,代入抛物线方程和圆的方程,可直接得到ABCD四个点的坐标,从而|AB||CD|=1.若直线的斜率存在,设为直线方程为y=k(x-1),不妨设A(x1,y1),D(x2,y2),过A、D分别作抛物线准线的垂线,由抛物线的定义,|AF|=x1+1,|DF|=x2+1,把直线方程与抛物线方程联立,消去y可得k2x2-(2k2+4)x+k2=0,利用韦达定理及|AB|=|AF|-|BF|=x1,|CD|=|DF|-|CF|=x2,可求|AB||CD|的值.
解:若直线的斜率不存在,则直线方程为x=1,代入抛物线方程和圆的方程,可直接得到ABCD四个点的坐标为(1,2)(1,1)(1,-1)(1,-2),所以|AB|=1,|CD|=1,从而|AB||CD|=1.若直线的斜率存在,设为k,因为直线过抛物线的焦点(1,0),则直线方程为y=k(x-1),不妨设A(x1,y1),D(x2,y2),过A、D分别作抛物线准线的垂线,由抛物线的定义,|AF|=x1+1,|DF|=x2+1,把直线方程与抛物线方程联立,消去y可得k2x2-(2k2+4)x+k2=0,由韦达定理有 x1x2=1而抛物线的焦点F同时是已知圆的圆心,所以|BF|=|CF|=R=1
从而有|AB|=|AF|-|BF|=x1,|CD|=|DF|-|CF|=x2.
所以|AB||CD|=x1x2=1
故选:A.


 星级口算天天练系列答案
星级口算天天练系列答案科目:高中数学 来源: 题型:
【题目】已知直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数)
为参数)
(Ⅰ)求直线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(Ⅱ)若过![]() 且与直线
且与直线![]() 垂直的直线
垂直的直线![]() 与曲线
与曲线![]() 相交于两点
相交于两点![]() ,
,![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是底面边长为1的正三棱锥,
是底面边长为1的正三棱锥,![]() 分别为棱长
分别为棱长![]() 上的点,截面
上的点,截面![]() 底面
底面![]() ,且棱台
,且棱台![]() 与棱锥
与棱锥![]() 的棱长和相等.(棱长和是指多面体中所有棱的长度之和)
的棱长和相等.(棱长和是指多面体中所有棱的长度之和)

(1)证明:![]() 为正四面体;
为正四面体;
(2)若![]() ,求二面角
,求二面角![]() 的大小;(结果用反三角函数值表示)
的大小;(结果用反三角函数值表示)
(3)设棱台![]() 的体积为
的体积为![]() ,是否存在体积为
,是否存在体积为![]() 且各棱长均相等的直平行六面体,使得它与棱台
且各棱长均相等的直平行六面体,使得它与棱台![]() 有相同的棱长和?若存在,请具体构造出这样的一个直平行六面体,并给出证明;若不存在,请说明理由.
有相同的棱长和?若存在,请具体构造出这样的一个直平行六面体,并给出证明;若不存在,请说明理由.
(注:用平行于底的截面截棱锥,该截面与底面之间的部分称为棱台,本题中棱台的体积等于棱锥![]() 的体积减去棱锥
的体积减去棱锥![]() 的体积.)
的体积.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场销售价与上市时间的关系用图(1)的一条折线表示;西红柿的种植成本与上市时间的关系用图(2)的抛物线段表示.


(1)写出图(1)表示的市场售价与时间的函数关系式![]() 写出图(2)表示的种植成本与时间的函数关系式
写出图(2)表示的种植成本与时间的函数关系式![]()
(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿收益最大?(注:市场售价和种植成本的单位:元/![]() kg,时间单位:天.)
kg,时间单位:天.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下列四个命题:
①等差数列一定是单调数列;
②等差数列的前![]() 项和构成的数列一定不是单调数列;
项和构成的数列一定不是单调数列;
③已知等比数列![]() 的公比为
的公比为![]() ,若
,若![]() ,则数列
,则数列![]() 是单调递增数列.
是单调递增数列.
④记等差数列的前![]() 项和为
项和为![]() ,若
,若![]() ,
,![]() ,则数列
,则数列![]() 的最大值一定在
的最大值一定在![]() 处达到.
处达到.
其中正确的命题有_____.(填写所有正确的命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】计划在某水库建一座至多安装3台发电机的水电站,过去50年的水文资料显示,水库年入流量X(年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上,其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年,如将年人流量在以上三段的频率作为相应段的概率,假设各年的年入流量相互独立.
(1)求未来4年中,至多有1年的年入流量超过120的概率;(![]() ,
,![]() )
)
(2)水电站希望安装的发电机尽可能运行最多,但每年发电机最多可运行台数受年入流量X限制,并有如下关系:
年流入量 |
|
|
|
发电机最多可运行台数 | 1 | 2 | 3 |
若某台发电机运行,则该台年利润为4000万元,若某台发电机未运行,则该台年亏损600万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一个容量为66的样本,数据的分组及各组的频数如下:
[10.5,14.5) 2 [14.5,18.5) 4 [18.5,22.5) 9 [22.5,26.5) 18
[26.5,30.5) 11 [30.5,34.5) 12 [34.5,38.5) 8 [38.5,42.5) 2
根据样本的频率分布估计,数据落在[30.5,42.5)内的概率约是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com