
分析 求得双曲线的渐近线方程,圆的圆心和半径,由直线和圆相切的条件:d=r,可得a2=8b2,再由a,b,c的关系和离心率公式计算即可得到所求值.
解答 解:双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的两条渐近线方程为y=±$\frac{b}{a}$x,
圆:(x-3)2+y2=1的圆心为(3,0),半径为1,
由直线和圆相切的条件可得,d=$\frac{3b}{\sqrt{{a}^{2}+{b}^{2}}}$=1,
化为a2=8b2,
由b2=c2-a2,可得8c2=9a2,
即有e2=$\frac{{c}^{2}}{{a}^{2}}$=$\frac{9}{8}$,
可得e=$\frac{3\sqrt{2}}{4}$.
故答案为:$\frac{3\sqrt{2}}{4}$.
点评 本题考查双曲线的离心率的求法,注意运用直线和圆相切的条件:d=r,考查点到直线的距离公式的运用,运算化简能力,属于中档题.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案科目:高中数学 来源: 题型:填空题
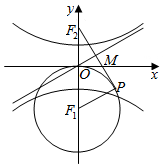 如图,已知F1,F2是双曲线$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1(a>0,b>0)的上下焦点,过F2点作以F1为圆心,|OF1|为半径的圆的切线,P为切点,若切线段PF2被一条渐近线平分,则双曲线的离心率为2.
如图,已知F1,F2是双曲线$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1(a>0,b>0)的上下焦点,过F2点作以F1为圆心,|OF1|为半径的圆的切线,P为切点,若切线段PF2被一条渐近线平分,则双曲线的离心率为2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{5}}{5}$ | B. | -$\frac{\sqrt{5}}{5}$i | C. | $\frac{\sqrt{5}}{5}$ | D. | -i |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5,15,25,35,45 | B. | 25,45,65,85,100 | C. | 10,30,50,70,90 | D. | 23,33,45,53,63 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{{\sqrt{2}}}{3}$,$\frac{{\sqrt{3}}}{3}$] | B. | [$\frac{1}{3}$,$\frac{1}{2}$] | C. | [$\frac{{\sqrt{3}}}{4}$,$\frac{{\sqrt{3}}}{3}$] | D. | [$\frac{1}{4}$,$\frac{1}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com