练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在平面直角坐标系xOy中，曲线C的参数方程为 （α为参数）以原点O为极点，x轴正半轴为极轴建立极坐标系，直线l的极坐标方程为 ．若直线l与曲线C交于A，B，求线段AB的长．

    【答案】解：由曲线C的参数方程为 （α为参数），
    利用cos2α+sin2α=1可得曲线C的普通方程为 ，表示以 为圆心，2为半径的圆．
    由直线l的极坐标方程为 ，可得直线l的直角坐标方程为 ，
    ∴圆心到直线的距离为 ，
    ∴线段AB的长为
    【解析】由曲线C的参数方程为 （α为参数），利用cos2α+sin2α=1可得曲线C的普通方程．由直线l的极坐标方程为 ，可得直线l的直角坐标方程．
    ∴圆心到直线的距离为 ，利用弦长公式即可得出．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知复数.

    (1)当实数m取什么值时,复数z是纯虚数?

    (2)若z在复平面内对应的点在第二、四象限的角平分线上,求|z|.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知各项均不为0的数列{an}满足a1=a，a2=b，且an2=an﹣1an+1+λ（n≥2，n∈N），其中λ∈R．
    （1）若λ=0，求证：数列{an}是等比数列；
    （2）求证：数列{an}是等差数列的充要条件是λ=（b﹣a）2；
    （3）若数列{bn}为各项均为正数的等比数列，且对任意的n∈N* ， 满足bn﹣an=1，求证：数列{（﹣1）nanbn}的前2n项和为常数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示,在四棱锥E-ABCD中,四边形ABCD是平行四边形,△BCE是等边三角形,△ABE是等腰直角三角形,∠BAE=90°,且AC=BC.

    (1)证明:平面ABE⊥平面BCE;

    (2)求二面角A-DE-C的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某宾馆在装修时，为了美观，欲将客房的窗户设计成半径为1m的圆形，并用四根木条将圆分成如图所示的9个区域，其中四边形ABCD为中心在圆心的矩形，现计划将矩形ABCD区域设计为可推拉的窗口．

    （1）若窗口ABCD为正方形，且面积大于 m2（木条宽度忽略不计），求四根木条总长的取值范围；
    （2）若四根木条总长为6m，求窗口ABCD面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】8人围圆桌开会，其中正、副组长各1人，记录员1人.

    (1)若正、副组长相邻而坐，有多少种坐法？

    (2)若记录员坐于正、副组长之间，有多少种坐法？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】从1到9这9个数字中取3个偶数和4个奇数,试问:

    (1)能组成多少个没有重复数字的七位数?

    (2)在(1)中的七位数中,偶数排在一起,奇数也排在一起的有多少个?

    (3)在(1)中任意2个偶数都不相邻的七位数有多少个?

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某商场在国庆黄金周的促销活动中，对10月1日9时至14时的销售额进行统计，其频率分布直方图如图所示．已知9时至10时的销售额为3万元，则11时至12时的销售额为万元．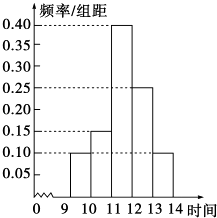

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公园准备在一圆形水池里设置两个观景喷泉，观景喷泉的示意图如图所示，A，B两点为喷泉，圆心O为AB的中点，其中OA=OB=a米，半径OC=10米，市民可位于水池边缘任意一点C处观赏．

    （1）若当∠OBC= 时，sin∠BCO= ，求此时a的值；
    （2）设y=CA2+CB2 ， 且CA2+CB2≤232．
    （i）试将y表示为a的函数，并求出a的取值范围；
    （ii）若同时要求市民在水池边缘任意一点C处观赏喷泉时，观赏角度∠ACB的最大值不小于 ，试求A，B两处喷泉间距离的最小值．

    查看答案和解析>>

    同步练习册答案