
分析 由题意画出图形,得到A的横坐标,代入椭圆方程求得A的纵坐标,结合$\overrightarrow{A{F_2}}$=3$\overrightarrow{{F_2}B}$求得B的坐标,代入椭圆方程整理得答案.
解答 解:如图,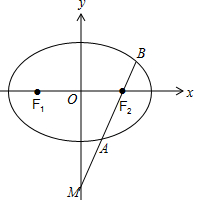
∵$\overrightarrow{MA}$=$\overrightarrow{A{F_2}}$,∴A为MF2的中点,则${x}_{A}=\frac{c}{2}$,
代入$\frac{{c}^{2}}{4{a}^{2}}+\frac{{{y}_{A}}^{2}}{{b}^{2}}=1$,得${{y}_{A}}^{2}=\frac{{b}^{2}(3{a}^{2}+{b}^{2})}{4{a}^{2}}$,∴${y}_{A}=-\frac{b}{2a}\sqrt{3{a}^{2}+{b}^{2}}$,
设B(xB,yB),则$\overrightarrow{A{F}_{2}}=(\frac{c}{2},\frac{b}{2a}\sqrt{3{a}^{2}+{b}^{2}})$,$\overrightarrow{{F}_{2}B}=({x}_{B}-c,{y}_{B})$,
由$\overrightarrow{A{F_2}}$=3$\overrightarrow{{F_2}B}$,得$\left\{\begin{array}{l}{\frac{c}{2}=3{x}_{B}-3c}\\{\frac{b}{2a}\sqrt{3{a}^{2}+{b}^{2}}=3{y}_{B}}\end{array}\right.$,即$\left\{\begin{array}{l}{{x}_{B}=\frac{7c}{6}}\\{{y}_{B}=\frac{b}{6a}\sqrt{3{a}^{2}+{b}^{2}}}\end{array}\right.$,
代入椭圆方程可得:$\frac{49{c}^{2}}{36{a}^{2}}+\frac{{b}^{2}(3{a}^{2}+{b}^{2})}{36{a}^{2}{b}^{2}}=1$,整理得:3c2=2a2,即$\frac{c}{a}=\frac{\sqrt{6}}{3}$.
故答案为:$\frac{\sqrt{6}}{3}$.
点评 本题考查椭圆的简单性质,考查了直线与椭圆位置关系的应用,训练了平面向量在求解圆锥曲线问题中的应用,是中档题.


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
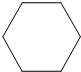 已知正六棱柱的底面边长和侧棱长相等,体积为96$\sqrt{3}$,其三视图中的俯视图如图所示,则其左视图的面积是( )
已知正六棱柱的底面边长和侧棱长相等,体积为96$\sqrt{3}$,其三视图中的俯视图如图所示,则其左视图的面积是( )| A. | $8\sqrt{3}$ | B. | 16 | C. | $16\sqrt{3}$ | D. | 32 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com