
分析 (Ⅰ)分情况将原不等式绝对值符号去掉,然后求解;
(Ⅱ)两边同除以|x|,然后求出左边的最小值,解关于m的不等式即可.
解答 解:(Ⅰ)当x≤$\frac{2}{3}$时,原不等式可化为-(3x-2)-(x-2)≤8,解得x≥-1,故此时-1≤x≤$\frac{2}{3}$;
当$\frac{2}{3}$<x≤2时,原不等式可化为3x-2-(x-2)≤8,解得x≤4,故此时$\frac{2}{3}$<x≤2;
当x>2时,原不等式可化为3x-2+x-2≤8,即x≤3,故此时2<x≤3.
综上可得,原不等式的解集为{x|-1≤x≤3}.
(Ⅱ)对任意的非零实数x,有f(x)≥(m2-m+2)•|x|恒成立,
则不等式可化为:m2-m+2≤|3-$\frac{2}{x}$|+|1-$\frac{2}{x}$|恒成立.
因为|3-$\frac{2}{x}$|+|1-$\frac{2}{x}$|≥|3-$\frac{2}{x}$+$\frac{2}{x}$-1|=2,
所以要使原式恒成立,只需m2-m+2≤2即可,即m2-m≤0.
解得0≤m≤1.
点评 本题考查了绝对值不等式的解法以及不等式恒成立问题的解题思路,一般的不等式恒成立问题要转化为函数的最值问题来解.本题还考查了分类讨论思想的应用.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
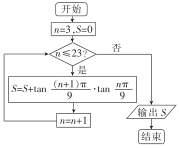
| A. | $-\frac{{2\sqrt{3}}}{{tan\frac{π}{9}}}-21$ | B. | $\frac{{tan\frac{25π}{9}-\sqrt{3}}}{{tan\frac{π}{9}}}-22$ | ||
| C. | $-\frac{{2\sqrt{3}}}{{tan\frac{π}{9}}}-22$ | D. | $\frac{{tan\frac{25π}{9}-\sqrt{3}}}{{tan\frac{π}{9}}}-21$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
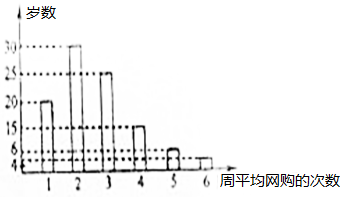 网购是当前民众购物的新方式,某公司为改进营销方式,随机调查了100名市民,统计其周平均网购的次数,并整理得到如下的频数直方图.这10名市民中,年龄不超过40岁的有65人.将所抽样中周平均网购次数不小于4次的市民称为网购迷,且已知其中有5名市民的年龄超过40岁.
网购是当前民众购物的新方式,某公司为改进营销方式,随机调查了100名市民,统计其周平均网购的次数,并整理得到如下的频数直方图.这10名市民中,年龄不超过40岁的有65人.将所抽样中周平均网购次数不小于4次的市民称为网购迷,且已知其中有5名市民的年龄超过40岁.| 网购迷 | 非网购迷 | 合计 | |
| 年龄不超过40岁 | |||
| 年龄超过40岁 | |||
| 合计 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,3) | B. | [3,5] | C. | (-3,5] | D. | (-∞,-3)∪[-2,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com