
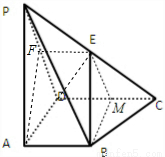
如图,四棱锥 的底面
的底面 为一直角梯形,侧面PAD是等边三角形,其中
为一直角梯形,侧面PAD是等边三角形,其中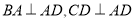 ,
, ,平面
,平面 底面
底面 ,
, 是
是 的中点.
的中点.

(1)求证: //平面
//平面 ;
;
(2)求证:
 ;
;
(3)求三棱锥 的体积
的体积 .
.
(1)祥见解析;(2)祥见解析;(3)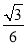 .
.
【解析】
试题分析:(1)证BE∥平面PAD,可先取CD的中点为M,构建平面EBM,证明平面EBM∥平面APD,由面面平行,得到线面平行;
(2)取PD的中点F,连接FE,根据线面垂直的判定及性质,及等腰三角形性质,结合线面垂直的判定定理可得AF⊥平面PDC,又由BE∥AF,可得BE⊥平面PDC;
(3)利用等体积法,由VP-ACD=VC-PAD,即可求三棱锥P-ACD的体积V.
试题解析:(1)证明:如图,
取PD的中点F,连接EF、AF,则在三角形PDC中
∴EF∥CD且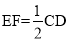 ,AB∥CD且
,AB∥CD且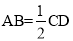 ;
;
∴EF∥AB且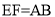 ,∴四边形ABEF是平行四边形, 2分
,∴四边形ABEF是平行四边形, 2分
∴BE∥AF,而BE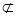 平面PAD,而AF?平面PAD,
平面PAD,而AF?平面PAD,
∴BE∥平面PAD; 4分
(2)证明:在直角梯形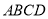 中,
中,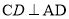
平面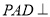 底面
底面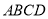 ,
,
平面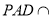 底面
底面 =AD
=AD
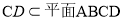
∴CD⊥平面PAD,
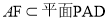 , ∴CD⊥AF
, ∴CD⊥AF
由(1)BE∥AF, ∴CD⊥BE 10分
(3)解:由(2)知∴CD⊥平面PAD,
△PAD是边长为1的等边三角形
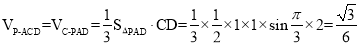
∴三棱锥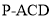 的体积
的体积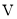 =
=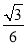 14分
14分
考点:1.直线与平面平行的判定;2.直线与平面垂直的判定;3.棱柱、棱锥、棱台的体积.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源:2015届广东省高二下学期期末考试文科数学试卷(解析版) 题型:选择题
在第29届北京奥运会上,中国健儿取得了51金、21银、28铜的好成绩,稳居金牌榜榜首,由此许多人认为中国进入了世界体育强国之列,也有许多人持反对意见,有网友为此进行了调查,在参加调查的2548名男性中有1560名持反对意见,2452名女性中有1200名持反对意见,在运用这些数据说明性别对判断“中国进入了世界体育强国之列”是否有关系时,用什么方法最有说服力( )
A.平均数与方差 B.回归直线方程 C.独立性检验 D.概率
查看答案和解析>>
科目:高中数学 来源:2015届广东省清远市高二下学期期末文科数学试卷(解析版) 题型:选择题
用反证法证明命题“若 a,b∈N,ab能被3整除,那么a,b中至少有一个能被3整除”时,假设应为( )
A.a,b都能被3整除 B.a不能被3整除
C.a,b不都能被3整除 D.a,b都不能被3整除
查看答案和解析>>
科目:高中数学 来源:2015届广东省高二下学期期末考试理科数学试卷(解析版) 题型:选择题
若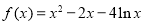 ,则
,则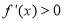 的解集为 ( )
的解集为 ( )
A.(0,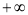 ) B.(-1,0)
) B.(-1,0)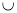 (2,
(2,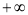 )
)
C.(2,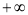 ) D.(-1,0)
) D.(-1,0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com