
| 1 |
| 2 |
| 1 |
| 2 |
| x |
| 4 |
| x |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| x |
| 4 |
| x |
| 2 |
| 3 |
| 2 |
| 5 |
| 4 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| x |
| 4 |
| x |
| 2 |
| 3 |
| 2 |
| 5 |
| 4 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 5 |
| 4 |
| 2 |
| 2 |
| 1 |
| 4 |


科目:高中数学 来源: 题型:
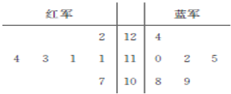 解放军某部在实兵演练对抗比赛中,红、蓝两个小组均派6人参加实弹射击,其所得成绩的茎叶图如图所示.
解放军某部在实兵演练对抗比赛中,红、蓝两个小组均派6人参加实弹射击,其所得成绩的茎叶图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| k-3 |
| y2 |
| k+3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |

| x2 |
| a2 |
| y2 |
| b2 |
| x0x |
| a2 |
| y0y |
| b2 |
| x2 |
| 8 |
| y2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 3 |
| π |
| 4 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,某观测站C在城A的南偏西20°方向上,从城A出发有一条公路,走向是南偏东40°.在C处测得距离C为31千米的公路上的B处有一辆车正沿着公路向城A驶去.该车行驶了20千米后到达D处停下,此时测得C、D两处距离为21千米.
如图,某观测站C在城A的南偏西20°方向上,从城A出发有一条公路,走向是南偏东40°.在C处测得距离C为31千米的公路上的B处有一辆车正沿着公路向城A驶去.该车行驶了20千米后到达D处停下,此时测得C、D两处距离为21千米.查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| π |
| 6 |
| π |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com