【题目】已知双曲线
： 
的左右焦点分别为
、
， 
为
右支上的点，线段
交
的左支于点
，若
是边长等于
的等边三角形，则双曲线的标准方程为（ ）
A. 
B. 
C. 
D. 
【答案】A
【解析】
即双曲线的标准方程为
，选A.
【题型】单选题
【结束】
11
【题目】张师傅欲将一球形的石材工件削砍加工成一圆柱形的新工件，已知原球形工件的半径为
，则张师傅的材料利用率的最大值等于（注：材料利用率=
）（ ）
A. 
B. 
C. 
D. 
科目：高中数学 来源： 题型：
【题目】一网站营销部为统计某市网友2017年12月12日在某网店的网购情况，随机抽查了该市60名网友在该网店的网购金额情况，如下表：
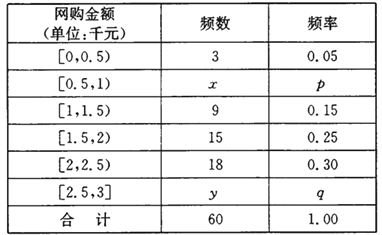
若将当日网购金额不小于2千元的网友称为“网购达人”，网购金额小于2千元的网友称为“网购探者”.已知“网购达人”与“网购探者”人数的比例为2：3.
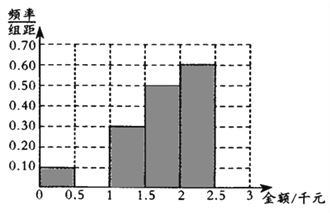
（1）确定
的值，并补全频率分布直方图；
（2）试根据频率分布直方图估算这60名网友当日在该网店网购金额的平均数和中位数；若平均数和中位数至少有一个不低于2千元，则该网店当日被评为“皇冠店”，试判断该网店当日能否被评为“皇冠店”.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=（a+2cos2x）cos（2x+θ）为奇函数，且f（ 
）=0，其中a∈R，θ∈（0，π）．
（1）求a，θ的值；
（2）若f（ 
）=﹣ 
，α∈（ 
，π），求sin（α+ 
）的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】张师傅欲将一球形的石材工件削砍加工成一圆柱形的新工件，已知原球形工件的半径为
，则张师傅的材料利用率的最大值等于（注：材料利用率=
）（ ）
A. 
B. 
C. 
D. 
【答案】C
【解析】设球半径为R，圆柱的体积为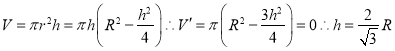
时圆柱的体积最大为
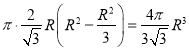,因此材料利用率=
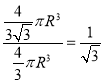,选C.
点睛:空间几何体与球接、切问题的求解方法
求解球与棱柱、棱锥的接、切问题时，一般过球心及接、切点作截面，把空间问题转化为平面图形与圆的接、切问题，再利用平面几何知识寻找几何中元素间的关系求解．
【题型】单选题
【结束】
12
【题目】已知抛物线
： 
在点
处的切线与曲线
： 
相切，若动直线
分别与曲线
、
相交于
、
两点，则
的最小值为（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知抛物线
： 
的焦点
为圆
的圆心.
（1）求抛物线
的标准方程；
（2）若斜率
的直线
过抛物线的焦点
与抛物线相交于
两点，求弦长
.
【答案】（1）
;（2）8.
【解析】试题分析：（1）先求圆心得焦点,根据焦点得抛物线方程（2）先根据点斜式得直线方程,与抛物线联立方程组,利用韦达定理以及弦长公式得弦长
.
试题解析：（1）圆的标准方程为
，圆心坐标为
，
即焦点坐标为
，得到抛物线
的方程： 
（2）直线
： 
，联立
，得到
弦长
【题型】解答题
【结束】
19
【题目】已知函数
在点
处的切线方程为
.
（1）求函数
的解析式；
（2）求函数
的单调区间和极值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】甲袋中有1只黑球，3只红球；乙袋中有2只黑球，1只红球.
(1)从甲袋中任取两球，求取出的两球颜色不相同的概率；
(2)从甲，乙两袋中各取一球，求取出的两球颜色相同的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】己知n为正整数，数列{an}满足an＞0，4（n+1）an2﹣nan+12=0，设数列{bn}满足bn= 
（1）求证：数列{ 
}为等比数列；
（2）若数列{bn}是等差数列，求实数t的值：
（3）若数列{bn}是等差数列，前n项和为Sn ， 对任意的n∈N* ， 均存在m∈N* ， 使得8a12Sn﹣a14n2=16bm成立，求满足条件的所有整数a1的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
