
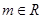 ,函数
,函数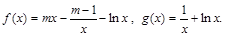
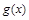 的极小值;
的极小值;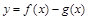 在
在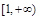 上为单调增函数,求
上为单调增函数,求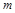 的取值范围;
的取值范围;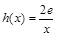 ,若在
,若在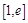 (
(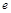 是自然对数的底数)上至少存在一个
是自然对数的底数)上至少存在一个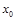 ,使得
,使得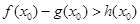 成立,求
成立,求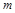 的取值范围.
的取值范围.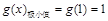 .(2)
.(2) 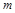 的取值范围是
的取值范围是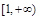 .
. 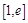 上存在一个
上存在一个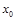 ,使得
,使得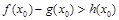 ,必须且只需
,必须且只需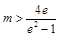 .
.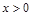 ,
, ,∴当
,∴当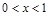 时,
时,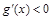 ;当
;当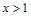 时,
时,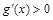 ,所以,
,所以,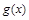 在
在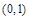 上是减函数,在
上是减函数,在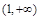 上是增函数,故
上是增函数,故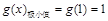 . 4分
. 4分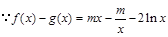 ,
,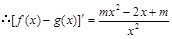 ,由于
,由于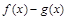 在
在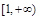 内为单调增函数,所以
内为单调增函数,所以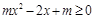 在
在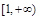 上恒成立,即
上恒成立,即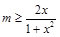 在
在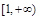 上恒成立,故
上恒成立,故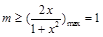 ,所以
,所以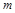 的取值范围是
的取值范围是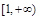 . 9分
. 9分 ,
,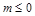 时,由
时,由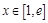 得,
得,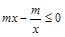 ,
,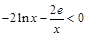 ,所以在
,所以在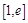 上不存在一个
上不存在一个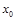 ,使得
,使得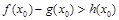 .
.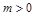 时,
时, ,因为
,因为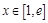 ,所以
,所以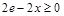 ,
,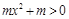 ,所以
,所以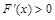 在
在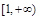 上恒成立,故
上恒成立,故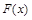 在
在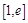 上单调递增,
上单调递增,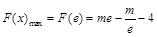 ,所以要在
,所以要在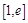 上存在一个
上存在一个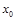 ,使得
,使得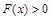 ,必须且只需
,必须且只需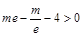 ,解得
,解得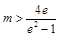 ,故
,故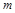 的取值范围是
的取值范围是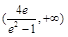 .
. 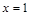 时,
时,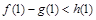 .
.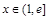 时,由
时,由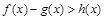 ,得
,得 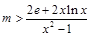 , 令
, 令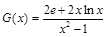 ,则
,则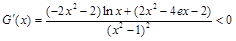 ,所以
,所以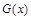 在
在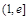 上递减,
上递减,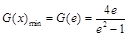 .
.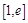 上存在一个
上存在一个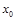 ,使得
,使得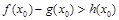 ,必须且只需
,必须且只需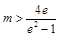 .
.

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com