
分析 确定直线l:kx-y+1=0(k∈R)过定点(0,1),曲线过定点(0,1),即可得出结论.
解答 解:①y=-|x|与直线l:kx-y+1=0(k∈R)至多一个交点,不具有性质P;
②x2+y2-2y=0圆心为(0,1),直线l:kx-y+1=0(k∈R)过定点(0,1),故存在k=±2,使直线l与曲线C交于A,B两点,且|AB|=|k|,具有性质P;
③y=(x+1)2,过点(0,1),直线l:kx-y+1=0(k∈R)过定点(0,1),故存在k,使直线l与曲线C交于A,B两点,且|AB|=|k|,具有性质P.
故答案为:②③.
点评 本题考查曲线与方程,考查新定义,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图的几何体中,AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2,F为CD的中点.
如图的几何体中,AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2,F为CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
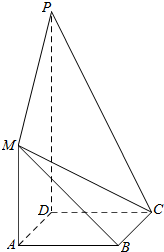 如图,正方形ABCD与梯形AMPD所在的平面互相垂直,AD⊥PD,MA∥PD,MA=AD=$\frac{1}{2}$PD=1.
如图,正方形ABCD与梯形AMPD所在的平面互相垂直,AD⊥PD,MA∥PD,MA=AD=$\frac{1}{2}$PD=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①④ | B. | ②④ | C. | ②③ | D. | ①③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=-4x+5 | B. | y=9-x2 | C. | y=($\frac{1}{2}$)x | D. | y=|x| |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com