Question

8．已知函数f（x）=sin$\frac{πx}{2}$（x∈R）．任取t∈R，若函数f（x）在区间[t，t+1]上的最大值为M（t），最小值为m（t），记g（t）=M（t）-m（t）．
（Ⅰ）求函数f（x）的最小正周期及对称轴方程
（Ⅱ）当t∈[-2，0]时，求函数g（t）的解析式
（Ⅲ）设函数h（x）=2^|x-k|，H（x）=x|x-k|+2k-8，其中实数k为参数，且满足关于t的不等式$\sqrt{2}$k-5g（t）≤0有解．若对任意x₁∈[4，+∞），存在x₂∈（-∞，4]，使得h（x₂）=H（x₁）成立，求实数k的取值范围
参考公式：sinα-cosα=$\sqrt{2}$sin（α-$\frac{π}{4}$）

Answer 1

分析 （Ⅰ）根据正弦函数的周期性和图象的对称性，求得函数f（x）的最小正周期及对称轴方程．
（Ⅱ）当t∈[-2，0]时，分类讨论求得M（t） 和m（t），可得g（t）的解析式．
（Ⅲ）由题意可得函数H（x）=x|x-k|+2k-8在[4，+∞）上的值域是h（x）在[4，+∞）上的值域的子集，分类讨论求得k的范围．

解答 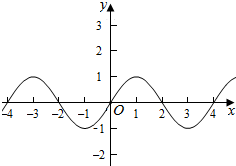解：（Ⅰ）对于函数f（x）=sin$\frac{πx}{2}$（x∈R），
它的最小正周期为$\frac{2π}{\frac{π}{2}}$=4，
由$\frac{πx}{2}$=kπ+$\frac{π}{2}$，求得x=2k+1，k∈Z，可得
f（x）的对称轴方程为x=2k+1，k∈Z．
（Ⅱ）当t∈[-2，0]时，
①若t∈[-2，-$\frac{3}{2}$），在区间[t，t+1]上，
M（t）=f（t）=sin$\frac{πt}{2}$，m（t）=f（-1）=-1，
g（t）=M（t）-m（t）=1+sin$\frac{πt}{2}$．
②若t∈[-$\frac{3}{2}$，-1），在区间[t，t+1]上，
M（t）=f（t+1）=sin$\frac{π}{2}$（t+1）=cos$\frac{π}{2}$t，m（t）=f（-1）=-1，
g（t）=M（t）-m（t）=1+cos$\frac{πt}{2}$．
③若t∈[-1，0]，在区间[t，t+1]上，
M（t）=f（t+1）=sin$\frac{π}{2}$（t+1）=cos$\frac{π}{2}$t，m（t）=f（t）=sin$\frac{π}{2}$t，
g（t）=M（t）-m（t）=cos$\frac{π}{2}$t-sin$\frac{πt}{2}$．
综上可得，g（t）=$\left\{\begin{array}{l}{1+sin\frac{π}{2}t，t∈[-2，-\frac{3}{2}）}\\{1+cos\frac{π}{2}t，t∈[-\frac{3}{2}，-1）}\\{cos\frac{πt}{2}-sin\frac{πt}{2}，t∈[-1，0]}\end{array}\right.$．
（Ⅲ）函数f（x）=sin$\frac{πx}{2}$的最小正周期为4，∴M（t+4）=M（t），m（t+4）=m（t）．
函数h（x）=2^|x-k|，H（x）=x|x-k|+2k-8，
对任意x₁∈[4，+∞），存在x₂∈（-∞，4]，使得h（x₂）=H（x₁）成立，
即函数H（x）=x|x-k|+2k-8在[4，+∞）上的值域是h（x）在[4，+∞）上的值域的子集．
∵h（x）=|2^|x-k|=$\left\{\begin{array}{l}{{2}^{x-k}，x≥k}\\{{2}^{k-x}，x＜k}\end{array}\right.$，
①当k≤4时，h（x）在（-∞，k）上单调递减，在[k，4]上单调递增．故h（x）的最小值为h（k）=1；
∵H（x）在[4，+∞）上单调递增，故H（x）的最小值为H（4）=8-2k．
由8-2k≥1，求得k≤$\frac{7}{2}$．
②当4＜k≤5时，h（x）在（-∞，4]上单调递减，h（x）的最小值为h（4）=2^k-4，
H（x）在[4，k]上单调递减，在（k，+∞）上单调递增，
故H（x）的最小值为H（k）=2k-8，由$\left\{\begin{array}{l}{4＜k≤5}\\{2k-8{≥2}^{k-4}}\end{array}\right.$，求得k=5，
综上可得，k的范围为（-∞，$\frac{7}{2}$]∪{5}．

点评 本题主要考查正弦函数的周期性，指数函数的图象特征，函数的能成立、函数的恒成立问题，属于难题．