
分析 (1)根据条件得出a2n+1=2Sn+n+4,①和a2n=2Sn-1+n+3,②,通过两式相减得到an+1=an+1,即为等差数列,再求bn的通项;
(2)先运用错位相减法求得cn的前n项和Tn,再用作差法判断单调性,最后求m的范围.
解答 (1))∵a2n+1=2Sn+n+4,------------①
∴n≥2时,a2n=2Sn-1+n-1+4,---------②
①-②,得:an+12-an2=2an+1,∴an+12=an2+2an+1=(an+1)2,
∵an>0,∴an+1=an+1,
因此,数列{an}是公差为1的等差数列,
又a2=a1+1,a22=2a1+1+4,解得a1=2或a1=-2(舍),
∴an=2+(n-1)×1=n+1.
∵a2-1,a3,a7恰为等比数列{bn}的前3项,
∴b1=2+1-1=2,b2=a3=3+1=4,b3=a7=7+1=8,∴q=2,
∴bn=2×2n-1=2n,
所以,an=n+1,bn=2n;
(2)根据题意,cn=$\frac{{a}_{n}-1}{{b}_{n}}$=$\frac{n}{2^n}$,
运用错位相减法得Tn=2-$\frac{n+2}{2^n}$,下面证明Tn单调递增,
Tn+1-Tn=(2-$\frac{n+3}{{2}^{n+1}}$)-(2-$\frac{n+2}{2^n}$)
=$\frac{1}{{2}^{n+1}}$[(2n+4)-(n+3)]
=$\frac{n+1}{{2}^{n+1}}$>0恒成立,所以,所以{Tn}单调递增,
所以,要使Tn>$\frac{m-1}{2}$恒成立,
只需满足T1>$\frac{m-1}{2}$即可,解得,m<2.
因此,实数m的取值范围为(-∞,2).
点评 本题主要考查了数列通项公式和前n项和的求法,涉及等差数列和等比数列的定义和性质,以及错位相减法的应用和单调性的证明,属于中档题.


科目:高中数学 来源: 题型:解答题
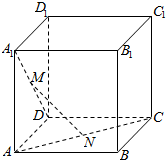 如图,在棱长为a的正方体ABCD-A1B1C1D1中,M为A1D中点,N为AC中点.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,M为A1D中点,N为AC中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 120° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com