
分析 由曲线方程的特点得到此曲线表示在x轴上方的圆的一半,可得出圆心坐标和圆的半径r,然后根据题意画出相应的图形,根据图形,直线y=k(x-3)+4,恒过(3,4),由图形过(3,4),(-3,0)的直线的斜率为$\frac{2}{3}$;
由圆心到直线的距离d=$\frac{|-3k+4|}{\sqrt{{k}^{2}+1}}$=3,可得直线与圆相切时,直线的斜率为$\frac{7}{24}$,综上,得到满足题意的k的范围.
解答 解:由题意可知:曲线方程表示一个在x轴上方的圆的一半,
则圆心坐标为(0,0),圆的半径r=3,
画出相应的图形,如图所示: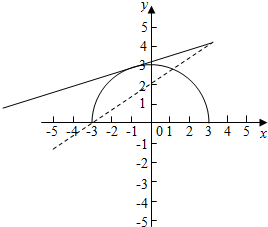
直线y=k(x-3)+4,恒过(3,4),由图形过(3,4),(-3,0)的直线的斜率为$\frac{2}{3}$;
由圆心到直线的距离d=$\frac{|-3k+4|}{\sqrt{{k}^{2}+1}}$=3,可得直线与圆相切时,直线的斜率为$\frac{7}{24}$.
综上,直线与曲线只有一个交点时,k的取值范围为$\left\{{\frac{7}{24}}\right\}∪({\frac{2}{3},+∞})$.
故答案为:$\left\{{\frac{7}{24}}\right\}∪({\frac{2}{3},+∞})$.
点评 此题考查了直线与圆相交的性质,考查数形结合的思想,根据题意得出此曲线表示在y轴右边的单位圆的一半,并画出相应的图形是解本题的关键.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,+∞) | B. | $(0,\frac{3}{4})$ | C. | $(\frac{3}{4},+∞)$ | D. | $[0,\frac{3}{4})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a<b,则ac<bc | B. | 若a<b,c<d,则ac<bd | ||
| C. | 若a<b<0,则$\frac{1}{a}$>$\frac{1}{b}$ | D. | 若a<b,则an<bn(n∈N*,n≥2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | $4+2\sqrt{5}$ | C. | $4\sqrt{5}$ | D. | $8\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com