
| A. | 30° | B. | 45° | C. | 120° | D. | 90° |
分析 做出相应图形,利用椭圆的简单性质得出A1B12+B1F22=A1F22,根据勾股定理判断得出∠A1B1F2的度数即可.
解答 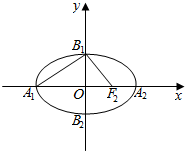 解:如图所示,A1F2=a+c,A1B12=a2+b2,B1F2=$\sqrt{{b}^{2}+{c}^{2}}$=a,
解:如图所示,A1F2=a+c,A1B12=a2+b2,B1F2=$\sqrt{{b}^{2}+{c}^{2}}$=a,
∵e=$\frac{c}{a}$=$\frac{\sqrt{5}-1}{2}$,
∴$\frac{{c}^{2}}{{a}^{2}}$=$\frac{3-\sqrt{5}}{2}$,a+c=$\frac{\sqrt{5}+1}{2}$a,
∴A1B12+B1F22=2a2+b2=3a2-c2=3a2-$\frac{3-\sqrt{5}}{2}$a2=$\frac{3+\sqrt{5}}{2}$a2,A1F22=(a+c)2=$\frac{3+\sqrt{5}}{2}$a2,
∴A1B12+B1F22=A1F22,
则∠A1B1F2=90°,
故选:D.
点评 此题考查了椭圆的简单性质,勾股定理的逆定理,熟练掌握椭圆的简单性质是解本题的关键.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a<b,则ac<bc | B. | 若a<b,c<d,则ac<bd | ||
| C. | 若a<b<0,则$\frac{1}{a}$>$\frac{1}{b}$ | D. | 若a<b,则an<bn(n∈N*,n≥2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com