
 在如图所示的几何体中,平面ADNM⊥平面ABCD,四边形ABCD是菱形,ADNM是矩形,$∠DAB=\frac{π}{3}$,AB=2,AM=1,E是AB的中点.
在如图所示的几何体中,平面ADNM⊥平面ABCD,四边形ABCD是菱形,ADNM是矩形,$∠DAB=\frac{π}{3}$,AB=2,AM=1,E是AB的中点.分析 (1)推导出DE⊥CD,ND⊥AD,从而ND⊥DE,进而DE⊥平面NDC,由此能证明平面MAE⊥平面NDC.
(2)以D为原点,建立空间直角坐标系D-xyz,求出平面PEC的一个法向量、平面ECD的法向量.利用向量的夹角公式,建立方程,即可得出结论.
解答 证明:(1)∵ABCD是菱形,∴AD=AB,∵∠DAB=60°,∴△ABD为等边三角形,
E为AB中点,∴DE⊥AB,∴DE⊥CD,
∵ADMN是矩形,∴ND⊥AD,
又平面ADMN⊥平面ABCD,平面ADMN∩平面ABCD=AD,
∴ND⊥平面ABCD,∴ND⊥DE,
∵CD∩ND=D,∴DE⊥平面NDC,
∵DE?平面MDE,∴平面MDE⊥平面NDC.
因为面ABM∥面NDC,∴平面DEM⊥平面ABM;
(2)解:设存在P符合题意.
由(Ⅰ)知,DE、DC、DN两两垂直,以D为原点,建立空间直角坐标系D-xyz(如图),
则D(0,0,0),A($\sqrt{3}$,-1,0),E($\sqrt{3}$,0,0),C(0,2,0),P($\sqrt{3}$,-1,h)(0≤h≤1).
∴$\overrightarrow{EP}$=(0,-1,h),$\overrightarrow{EC}$=(-$\sqrt{3}$,2,0),设平面PEC的法向量为$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{EP}=-y+hz=0}\\{\overrightarrow{n}•\overrightarrow{EC}=-\sqrt{3}x+2y=0}\end{array}\right.$令x=2h,则平面PEC的一个法向量为$\overrightarrow{n}$=(2h,$\sqrt{3}$h,$\sqrt{3}$)
取平面ECD的法向量$\overrightarrow{m}$=(0,0,1),
cos45°=$\frac{\sqrt{3}}{\sqrt{7{h}^{2}+3}}$,解得h=$\frac{\sqrt{21}}{7}$∈[0,1],
即存在点P,使二面角P-EC-D的大小为$\frac{π}{4}$,此时AP=$\frac{\sqrt{21}}{7}$.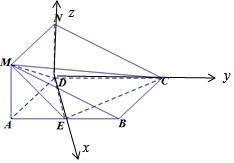
点评 本题考查线面垂直,考查二面角,考查向量法的运用,考查学生分析解决问题的能力,属于中档题


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
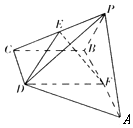 如图,在四棱锥P-ABCD中底面ABCD是直角梯形,AB∥CD,∠ABC=90°,AB=2CD,BC=$\sqrt{3}$CD,△APB是等边三角形,且侧面APB⊥底面ABCD,E,F分别是PC,AB的中点.
如图,在四棱锥P-ABCD中底面ABCD是直角梯形,AB∥CD,∠ABC=90°,AB=2CD,BC=$\sqrt{3}$CD,△APB是等边三角形,且侧面APB⊥底面ABCD,E,F分别是PC,AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图1,以BD为直径的圆O经过A,C两点,延长DA,CB交于P点,如图2,将PAB沿线段AB折起,使P点在底面ABCD的射影恰为AD的中点Q,AB=BC=1,BD=2,线段PB,PC的中点为E,F.
如图1,以BD为直径的圆O经过A,C两点,延长DA,CB交于P点,如图2,将PAB沿线段AB折起,使P点在底面ABCD的射影恰为AD的中点Q,AB=BC=1,BD=2,线段PB,PC的中点为E,F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
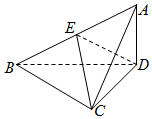 已知三棱锥A-BCD中,△ABC是等腰直角三角形,且AC⊥BC,BC=2,AD⊥平面BCD,AD=1.
已知三棱锥A-BCD中,△ABC是等腰直角三角形,且AC⊥BC,BC=2,AD⊥平面BCD,AD=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=-sin2x | B. | f(x)的图象关于x=-$\frac{π}{3}$对称 | ||
| C. | f($\frac{7π}{3}$)=$\frac{1}{2}$ | D. | f(x)的图象关于($\frac{π}{12}$,0)对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-2≤x≤4} | B. | {x|x≥1} | C. | {x|1≤x≤4} | D. | {x|x≥-2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com