
| A. | $\frac{\sqrt{2}}{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | -$\frac{\sqrt{5}}{5}$ |
分析 由向量的加法、减法法则和向量的坐标运算求出$\overrightarrow{OB}$、$\overrightarrow{AC}$的坐标,再利用向量的数量积运算求出$\overrightarrow{OB}$与$\overrightarrow{AC}$夹角的余弦.
解答 解:因为在平行四边形OABC中,$\overrightarrow{OA}$=(4,2),$\overrightarrow{OC}$=(2,6),
所以$\overrightarrow{OB}$=$\overrightarrow{OA}+\overrightarrow{OC}$=(6,8),$\overrightarrow{AC}$=$\overrightarrow{OC}-\overrightarrow{OA}$=(-2,4),
设$\overrightarrow{OB}$与$\overrightarrow{AC}$夹角是θ,
则cosθ=$\frac{\overrightarrow{OB}•\overrightarrow{AC}}{|\overrightarrow{OB}||\overrightarrow{AC}|}$=$\frac{-12+32}{\sqrt{{6}^{2}+{8}^{2}}×\sqrt{{2}^{2}+{4}^{2}}}$=$\frac{20}{10×2\sqrt{5}}$=$\frac{\sqrt{5}}{5}$,
故选:C.
点评 本题考查利用向量的数量积运算求向量夹角的余弦值,向量的加法、减法法则,以及向量的坐标运算,属于中档题.


科目:高中数学 来源:2017届河北武邑中学高三上周考8.14数学(理)试卷(解析版) 题型:选择题
若对正常数 和任意实数
和任意实数 ,等式
,等式 成立,则下列说法正确的是( )
成立,则下列说法正确的是( )
A.函数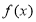 是周期函数,最小正周期为
是周期函数,最小正周期为
B.函数 是奇函数,但不是周期函数
是奇函数,但不是周期函数
C.函数 是周期函数,最小正周期为
是周期函数,最小正周期为
D.函数 是偶函数,但不是周期函数
是偶函数,但不是周期函数
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,3] | B. | (-∞,-3) | C. | [-3,1]∪(3,+∞) | D. | (-∞,1]∪(3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日期 | 1月11日 | 1月12日 | 1月13日 | 1月14日 | 1月15日 |
| 平均气温x( ) | 9 | 10 | 12 | 11 | 8 |
| 销量y(杯) | 23 | 25 | 30 | 26 | 21 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1) | B. | (-1,3) | C. | (-∞,3) | D. | (3,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com