
| A. | $[\sqrt{5},2\sqrt{5}]$ | B. | $[\sqrt{5},2\sqrt{10})$ | C. | $(\sqrt{5},\sqrt{10})$ | D. | $[\sqrt{5},2\sqrt{10}]$ |
分析 根据题意,由向量的坐标运算公式可得$\overrightarrow{OC}=m\overrightarrow{OA}-n\overrightarrow{OB}$=(3m+n,m-3n),再由向量模的计算公式可得$|\overrightarrow{OC}|$=$\sqrt{10({m}^{2}+{n}^{2})}$,可以令t=$\sqrt{{m}^{2}+{n}^{2}}$,将m+n∈[1,2]的关系在直角坐标系表示出来,分析可得t=$\sqrt{{m}^{2}+{n}^{2}}$表示区域中任意一点与原点(0,0)的距离,进而可得t的取值范围,又由$|\overrightarrow{OC}|$=$\sqrt{10}$t,分析可得答案.
解答 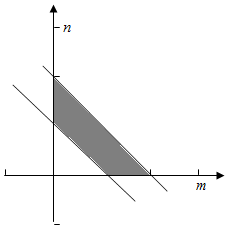 解:根据题意,向量$\overrightarrow{OA}=(3,1)$,$\overrightarrow{OB}=(-1,3)$,
解:根据题意,向量$\overrightarrow{OA}=(3,1)$,$\overrightarrow{OB}=(-1,3)$,
$\overrightarrow{OC}=m\overrightarrow{OA}-n\overrightarrow{OB}$=(3m+n,m-3n),
则$|\overrightarrow{OC}|$=$\sqrt{(3m+n)^{2}+(m-3n)^{2}}$=$\sqrt{10({m}^{2}+{n}^{2})}$,
令t=$\sqrt{{m}^{2}+{n}^{2}}$,则$|\overrightarrow{OC}|$=$\sqrt{10}$t,
而m+n∈[1,2],即1≤m+n≤2,在直角坐标系表示如图,
t=$\sqrt{{m}^{2}+{n}^{2}}$表示区域中任意一点与原点(0,0)的距离,
分析可得:$\frac{\sqrt{2}}{2}$≤t<2,
又由$|\overrightarrow{OC}|$=$\sqrt{10}$t,
故$\sqrt{5}$≤$|\overrightarrow{OC}|$<2$\sqrt{10}$;
故选:B.
点评 本题考查简单线性规划问题,涉及向量的模的计算,关键是求出$|\overrightarrow{OC}|$的表达式.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
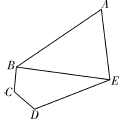 某学校的平面示意图为如下图五边形区域ABCDE,其中三角形区域ABE为生活区,四边形区域BCDE为教学区,AB,BC,CD,DE,EA,BE为学校的主要道路(不考虑宽度).$∠BCD=∠CDE=\frac{2π}{3}$,$∠BAE=\frac{π}{3},DE=3BC=3CD=\frac{9}{10}km$.
某学校的平面示意图为如下图五边形区域ABCDE,其中三角形区域ABE为生活区,四边形区域BCDE为教学区,AB,BC,CD,DE,EA,BE为学校的主要道路(不考虑宽度).$∠BCD=∠CDE=\frac{2π}{3}$,$∠BAE=\frac{π}{3},DE=3BC=3CD=\frac{9}{10}km$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|1<x<3} | B. | {x|-1<x<3} | C. | {x|-1<x<0或0<x<3} | D. | {x|-1<x<0或1<x<3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AD=AP,E为棱PD中点.
如图,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AD=AP,E为棱PD中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[\sqrt{7},3)$ | B. | $[1,\sqrt{7})$ | C. | $[\sqrt{5},3)$ | D. | $[\sqrt{5},\sqrt{7})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c>b>a | B. | a>c>b | C. | a>b>c | D. | b>c>a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com