
| A. | $[\sqrt{7},3)$ | B. | $[1,\sqrt{7})$ | C. | $[\sqrt{5},3)$ | D. | $[\sqrt{5},\sqrt{7})$ |
分析 由题意设θ=$∠PQ{F_2}∈[\frac{π}{3},π)$,可得∠F1PF2=$\frac{π+θ}{2}$,设|QP|=|QF2|=x,则由双曲线的定义可得|PF1|=2a,即有|PF2|=4a,在△PF1F2中,运用余弦定理和诱导公式,以及离心率公式,解不等式即可得到e的范围.
解答 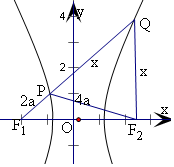 解:△PQF2是以∠PQF2为顶角的等腰三角形,
解:△PQF2是以∠PQF2为顶角的等腰三角形,
其中设θ=$∠PQ{F_2}∈[\frac{π}{3},π)$,
可得∠F1PF2=$\frac{π+θ}{2}$,
设|QP|=|QF2|=x,
则由双曲线的定义可得|QF1|-|QF2|=2a,即|PF1|=2a,
即有|PF2|=4a,
在△PF1F2中,由余弦定理可得,cos∠F1PF2=$\frac{4{a}^{2}+16{a}^{2}-4{c}^{2}}{2•2a•4a}$
=$\frac{5}{4}$-$\frac{1}{4}$e2=-sin$\frac{θ}{2}$∈(-1,-$\frac{1}{2}$],
解得$\sqrt{7}$≤e<3.
故选:A.
点评 本题考查双曲线的定义、方程和性质,考查余弦定理和诱导公式的运用,以及正弦函数的图象和性质,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $[\sqrt{5},2\sqrt{5}]$ | B. | $[\sqrt{5},2\sqrt{10})$ | C. | $(\sqrt{5},\sqrt{10})$ | D. | $[\sqrt{5},2\sqrt{10}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
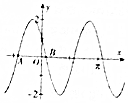 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示,其中A(-$\frac{5π}{12}$,0),B($\frac{π}{12}$,0),则函数f(x)的单调增区间为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示,其中A(-$\frac{5π}{12}$,0),B($\frac{π}{12}$,0),则函数f(x)的单调增区间为( )| A. | [-$\frac{π}{6}$+kπ,$\frac{π}{3}$+kπ](k∈Z) | B. | [$\frac{π}{3}$+kπ,$\frac{5π}{6}$+kπ](k∈Z) | ||
| C. | [-$\frac{π}{6}$+2kπ,$\frac{π}{3}$+2kπ](k∈Z) | D. | [$\frac{π}{3}$+2kπ,$\frac{5π}{6}$+2kπ](k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 每年的4月23日为世界读书日,为调查某高校学生(学生很多)的读书情况,随机抽取了男生,女生各20人组成的一个样本,对他们的年阅读量(单位:本)进行了统计,分析得到了男生年阅读量的频率分布表和女生阅读量的频率分布直方图.
每年的4月23日为世界读书日,为调查某高校学生(学生很多)的读书情况,随机抽取了男生,女生各20人组成的一个样本,对他们的年阅读量(单位:本)进行了统计,分析得到了男生年阅读量的频率分布表和女生阅读量的频率分布直方图.| 本/年 | [0,10) | [10,20) | [20,30) | [30,40) | [40,50) | [50,60] |
| 频数 | 3 | 1 | 8 | 4 | 2 | 2 |
| 性别 阅读量 | 丰富 | 不丰富 | 合计 |
| 男 | |||
| 女 | |||
| 合计 |
| P(K2≥k0) | 0.025 | 0.010 | 0.005 |
| k0 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如甲图所示,在矩形ABCD中,AB=4,AD=2,E是CD的中点,将△ADE沿AE折起到△D1AE位置,使平面D1AE⊥平面ABCE,得到乙图所示的四棱锥D1-ABCE.
如甲图所示,在矩形ABCD中,AB=4,AD=2,E是CD的中点,将△ADE沿AE折起到△D1AE位置,使平面D1AE⊥平面ABCE,得到乙图所示的四棱锥D1-ABCE.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {8,10} | B. | {8,12} | C. | {8,14} | D. | {8,10,14} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
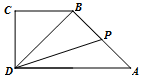 如图,在直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=2,BC=CD=1,P是AB的中点,则$\overrightarrow{DP}•\overrightarrow{AB}$=-1.
如图,在直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=2,BC=CD=1,P是AB的中点,则$\overrightarrow{DP}•\overrightarrow{AB}$=-1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com