
分析 作差可知x0≥-$\frac{m+1}{2}$时,f(x0+1)≥f(x0).从而化为f(x0+1)=(x0+1)2+m(x0+1)+$\frac{3}{4}$=x02+(m+2)x0+$\frac{7}{4}$+m在x0≥-$\frac{m+1}{2}$,f(x0+1)min=(-$\frac{m+1}{2}$+$\frac{m+2}{2}$)2+$\frac{7}{4}$+m-($\frac{m+2}{2}$)2≥0恒成立,可得|m|≤2,即可得出结论.
解答 解:∵f(x0+1)-f(x0)=(x0+1)2+m(x0+1)+$\frac{3}{4}$-(x02+mx0+$\frac{3}{4}$)=2x0+m+1,
∴当2x0+m+1≥0,即x0≥-$\frac{m+1}{2}$时,f(x0+1)≥f(x0).
而f(x0+1)=(x0+1)2+m(x0+1)+$\frac{3}{4}$=x02+(m+2)x0+$\frac{7}{4}$+m,
∵-$\frac{m+1}{2}$>-$\frac{m+2}{2}$,
∴f(x0+1)min=(-$\frac{m+1}{2}$+$\frac{m+2}{2}$)2+$\frac{7}{4}$+m-($\frac{m+2}{2}$)2≥0恒成立,
即m2≤4恒成立,
故|m|≤2,
∴-2≤m≤2.
故答案为:-2≤m≤2.
点评 本题考查了分类讨论的思想应用及作差法的应用,属于中档题.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
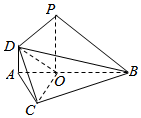 如图$∠ABC=\frac{π}{4},O$为AB上一点,且3OB=3OC=2AB,又PO⊥平面ABC,2DA=2AO=PO,且DA∥PO.
如图$∠ABC=\frac{π}{4},O$为AB上一点,且3OB=3OC=2AB,又PO⊥平面ABC,2DA=2AO=PO,且DA∥PO.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (-∞,1)∪(2,+∞) | C. | (-$\frac{2}{3}$,1) | D. | (-∞,-$\frac{2}{3}$)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5条; | B. | 4条 | C. | 3条 | D. | 2条 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com