
分析 f(x)解析式利用诱导公式,二倍角的正弦、余弦函数公式化为一个角的正弦函数,找出ω的值,代入周期公式求出最小正周期;根据x的范围求出值域即可.
解答 解:f(x)=cosxsinx-$\sqrt{3}$cos2x+$\frac{\sqrt{3}}{2}$=$\frac{1}{2}$sin2x-$\frac{\sqrt{3}}{2}$cos2x=sin(2x-$\frac{π}{3}$),
∵ω=2,∴T=$\frac{2π}{2}$=π,
∵$\frac{π}{6}$≤x≤$\frac{2π}{3}$,
∴0≤2x-$\frac{π}{3}$≤π,即0≤sin(2x-$\frac{π}{3}$)≤1,
则f(x)在[$\frac{π}{6}$,$\frac{2π}{3}$]上的值域为[0,1],
故答案为:π,[0,1]
点评 此题考查了三角函数中的恒等变换应用,以及三角函数的周期性及其求法,熟练掌握运算法则及公式是解本题的关键.


科目:高中数学 来源: 题型:选择题
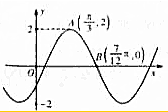 函数f(x)=asinωx+bcosωx(ω>0)的图象如图所示,则a,b的取值范围分别为( )
函数f(x)=asinωx+bcosωx(ω>0)的图象如图所示,则a,b的取值范围分别为( )| A. | $\sqrt{3},1$ | B. | $-\sqrt{3},1$ | C. | $\sqrt{3},-1$ | D. | -3,-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
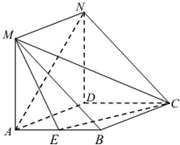 在如图所示的几何体中,四边形ABCD是边长为2的正方形,ADNM是矩形,平面ADNM⊥平面ABCD,AM=1,E是AB的中点,
在如图所示的几何体中,四边形ABCD是边长为2的正方形,ADNM是矩形,平面ADNM⊥平面ABCD,AM=1,E是AB的中点,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 9 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-\frac{π}{6}+kπ,\frac{π}{6}+kπ)k∈Z$ | B. | $(-\frac{π}{6}+kπ,\frac{π}{3}+kπ)k∈Z$ | C. | $(-\frac{π}{2}+kπ,\frac{π}{6}+kπ)k∈Z$ | D. | $(-\frac{π}{6}+kπ,\frac{π}{2}+kπ)k∈Z$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某几何体的三视图如图所示,P是正方形ABCD对角线的交点,G是PB的中点.
某几何体的三视图如图所示,P是正方形ABCD对角线的交点,G是PB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com