
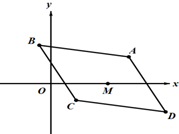
 如图,平行四边形ABCD(A,B,C,D按逆时针顺序排列),AB,AD边所在直线的方程分别是x+4y-7=0,3x+2y-11=0,且对角线AC和BD的交点为M(2,0)
如图,平行四边形ABCD(A,B,C,D按逆时针顺序排列),AB,AD边所在直线的方程分别是x+4y-7=0,3x+2y-11=0,且对角线AC和BD的交点为M(2,0)分析 (1)联立直线方程,解方程组可得交点A;
(2)解法一:求出C(1,-1),由平行关系可得直线CD的斜率,可得点斜式方程,化为一般式即可;
解法二:C(1,-1),设CD边所在的直线方程为:x+4y+m=0,代点求m即可;
解法三:设P(x,y)为CD边所在的直线上的任一点,P关于点M的对称点为P′(x0,y0),代入法消参数可得.
解答 解:(1)由题意联立直线方程$\left\{\begin{array}{l}x+4y-7=0\\ 3x+2y-11=0\end{array}\right.$,
解方程组可得$\left\{\begin{array}{l}x=3\\ y=1\end{array}\right.$,∴A(3,1)
(2)解法一:A关于M的对称点为C,∴C(1,-1),
又${k_{AB}}={k_{CD}}=-\frac{1}{4}$,∴CD边所在的直线方程为$y+1=-\frac{1}{4}(x-1)$
化为一般式可得:x+4y+3=0
解法二:A关于M的对称点为C,∴C(1,-1),
设CD边所在的直线方程为:x+4y+m=0,
∴1+4×(-1)+m=0,解得m=3,
∴CD边所在的直线方程为x+4y+3=0
解法三:设P(x,y)为CD边所在的直线上的任一点,
P关于点M的对称点为P′(x0,y0),
则$\left\{\begin{array}{l}\frac{{x+{x_0}}}{2}=2\\ \frac{{y+{y_0}}}{2}=0\end{array}\right.$,解得$\left\{\begin{array}{l}{x_0}=4-x\\{y_0}=-y\end{array}\right.$,
又P′在直线AB上,∴(4-x)+4(-y)-7=0
∴x+4y+3=0
点评 本题考查直线的方程,直线与直线的位置关系,点线对称关系等基础知识,属基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
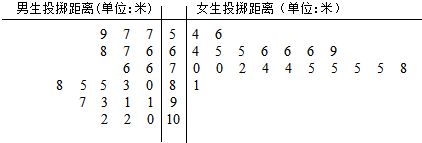
| 男生投掷距离(米) | … | [5.4,6.0) | [6.0,6.6) | [6.6,7.4) | [7.4,7.8) | [7.8,8.6) | [8.6,10.0) | [10.0,+∞) |
| 女生投掷距离(米) | … | [5.1,5.4) | [5.4,5.6) | [5.6,6.4) | [6.4,6.8) | [6.8,7.2) | [7.2,7.6) | [7.6,+∞) |
| 个人得分(分) | … | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,0) | B. | (-2,-1)∪(-1,0) | C. | (-∞,-2)∪(0,+∞) | D. | (0,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com