
分析 (1)根据所给结论,可写出一个一般性的命题.
(2)利用综合法证明命题是真命题.
解答 解:(1)一般性的命题n是正整数,则$\sqrt{n+1}$-$\sqrt{n}$>$\sqrt{n+2}$-$\sqrt{n+1}$.
(2)命题是真命题.
∵$\sqrt{n+1}$-$\sqrt{n}$=$\frac{1}{\sqrt{n+1}+\sqrt{n}}$,$\sqrt{n+2}$-$\sqrt{n+1}$=$\frac{1}{\sqrt{n+2}+\sqrt{n+1}}$,$\frac{1}{\sqrt{n+1}+\sqrt{n}}$>$\frac{1}{\sqrt{n+2}+\sqrt{n+1}}$,
∴$\sqrt{n+1}$-$\sqrt{n}$>$\sqrt{n+2}$-$\sqrt{n+1}$.
点评 本题考查归纳推理,考查综合法的运用,属于基础题.


 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:解答题
 某公司为确定2017年度投入某种产品的宣传费,需了解年宣传费x(单位:万元)对年销售收益y(单位:万元)的影响,2016年在若干地区各投入4万元的宣传费,并将各地的销售收益的数据作了初步处理,得到下面的频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.
某公司为确定2017年度投入某种产品的宣传费,需了解年宣传费x(单位:万元)对年销售收益y(单位:万元)的影响,2016年在若干地区各投入4万元的宣传费,并将各地的销售收益的数据作了初步处理,得到下面的频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.| 宣传费x(单位:万元) | 3 | 2 | 1 | 5 | 4 |
| 销售收益y(单位:万元) | 2 | 3 | 2 | 7 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $x=\frac{kπ}{2}+\frac{π}{12}({k∈Z})$ | B. | $x=\frac{kπ}{2}+\frac{π}{8}({k∈Z})$ | C. | $x=kπ+\frac{π}{12}({k∈Z})$ | D. | $x=kπ+\frac{π}{8}({k∈Z})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (4,$\frac{5π}{6}$) | B. | (4,$\frac{2π}{3}$) | C. | (4,$\frac{5π}{3}$) | D. | (4,$\frac{11π}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
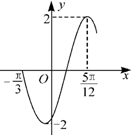
| A. | $2\;,\;\frac{2π}{3}$ | B. | $2\;,\;-\frac{π}{3}$ | C. | $1\;,\;\frac{π}{12}$ | D. | $1\;,\;-\frac{π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com