
 ij��˾Ϊȷ��2017���Ͷ��ij�ֲ�Ʒ�������ѣ����˽���������x����λ����Ԫ��������������y����λ����Ԫ����Ӱ�죬2016�������ɵ�����Ͷ��4��Ԫ�������ѣ��������ص�����������������˳����������õ������Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ�������ڹ�����Ա����ʧ��������ݶ�ʧ��������ȷ�������Ǵ�0��ʼ�����ģ�
ij��˾Ϊȷ��2017���Ͷ��ij�ֲ�Ʒ�������ѣ����˽���������x����λ����Ԫ��������������y����λ����Ԫ����Ӱ�죬2016�������ɵ�����Ͷ��4��Ԫ�������ѣ��������ص�����������������˳����������õ������Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ�������ڹ�����Ա����ʧ��������ݶ�ʧ��������ȷ�������Ǵ�0��ʼ�����ģ�| ������x����λ����Ԫ�� | 3 | 2 | 1 | 5 | 4 |
| ��������y����λ����Ԫ�� | 2 | 3 | 2 | 7 | 5 |
���� �������С�����εĿ���Ϊm�����m���ɵø������е�ֵ�����ɹ���ƽ��ֵ
��������ع�ϵ������������ع鷽�̣�
����x=10ʱ��y=12.2���ɵý��ۣ�
��� �⣺�������С�����εĿ���Ϊm����0.08+0.10+0.14+0.12+0.04+0.02��m=1����m=2��
�������е�ֵ�ֱ�Ϊ1��3��5��7��9��11����Ӧ��Ƶ�ʷֱ�Ϊ0.16��0.20��0.28��0.24��0.08��0.04��
����ƽ��ֵΪ1��0.16+3��0.20+5��0.28+7��0.24+9��0.08+11��0.04=5��
���������⣬$\overline{x}$=3��$\overline{y}$=3.8��$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$=��$\frac{69-5��3��3.8}{55-5��9}$=1.2��$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$=3.8-1.2��3=0.2��
��y����x�Ļع�ֱ�߷���y=1.2x+0.2��
����x=10ʱ��y=12.2����������Ͷ��Ϊ10��Ԫʱ�����������ԼΪ12.2��Ԫ��
���� ���⿼��ع鷽�̵ļ��������ã�����Ƶ�ʷֲ�ֱ��ͼ�������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
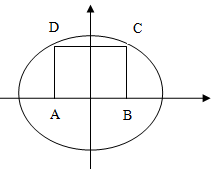 ��ͼ����Ϊ2$\sqrt{3}$����Ϊ$\frac{1}{2}$�ľ���ABCD����A��BΪ�������ԲM��$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1ǡ�ù�C��D���㣮
��ͼ����Ϊ2$\sqrt{3}$����Ϊ$\frac{1}{2}$�ľ���ABCD����A��BΪ�������ԲM��$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1ǡ�ù�C��D���㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | $\frac{5}{2}$ | C�� | 2 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | $\sqrt{2}$ | C�� | $\frac{{\sqrt{11}}}{3}$ | D�� | $\frac{{2\sqrt{5}}}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | R | B�� | ��-�ޣ�2�� | C�� | ��1��2�� | D�� | [1��2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com