
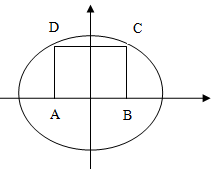
 如图,长为2$\sqrt{3}$,宽为$\frac{1}{2}$的矩形ABCD,以A、B为焦点的椭圆M:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1恰好过C、D两点.
如图,长为2$\sqrt{3}$,宽为$\frac{1}{2}$的矩形ABCD,以A、B为焦点的椭圆M:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1恰好过C、D两点.分析 (1)设B(c,0),推出C(c,$\frac{b^2}{a}$)利用已知条件列出方程组即可求解M的方程.
(2)将l:y=kx+3代入 $\frac{{x}^{2}}{4}$+y2=1,利用韦达定理以及弦长公式,点到平面的距离的距离,表示三角形的面积,利用基本不等式求解即可.
解答 (1)设B(c,0),由条件知,C(c,$\frac{b^2}{a}$).(1分)
∴$\left\{\begin{array}{l}\frac{b^2}{a}=\frac{1}{2}\\ c=\sqrt{3}\\{a^2}={b^2}+{c^2}\end{array}\right.$,解得a=2,b=(3分)
故M的方程为 $\frac{{x}^{2}}{4}$+y2=1.(4分)
(2)将l:y=kx+3代入 $\frac{{x}^{2}}{4}$+y2=1
(1+4k2)x2+24kx+32=0.(5分)
当△=64(k2-2)>0,即k2>2时,(6分)
从而|PQ|=$\sqrt{1+{k}^{2}}$|x1-x2|=$\sqrt{1+{k^2}}•\frac{{\sqrt{64({k^2}-2)}}}{{4{k^2}+1}}$.(7分)
又点O到直线PQ的距离d=$\frac{3}{{\sqrt{{k^2}+1}}}$,(8分)
所以△POQ的面积S△OPQ=$\frac{1}{2}$d|PQ|=$\frac{{12\sqrt{{k^2}-2}}}{{4{k^2}+1}}$.(9分)
设$\sqrt{{k^2}-2}$=t,则t>0,S△OPQ=$\frac{12t}{{4{t^2}+9}}=\frac{12}{{4t+\frac{9}{t}}}≤\frac{12}{{2\sqrt{4t•\frac{9}{t}}}}=1$.
当且仅当t=$\frac{3}{2}$时等号成立,且满足△>0,
所以,△POQ的面积最大值为1(12分)
点评 本题考查直线与椭圆的位置关系的应用,基本不等式的应用,考查转化思想以及计算能力.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | {0,1} | B. | (0,1) | C. | [-3,-1)∪(2,3] | D. | {-3,-2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-3)∪(1,+∞) | B. | (-∞,-3)∪(1,2] | C. | (-∞,-3)∪[0,+∞) | D. | (1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某公司为确定2017年度投入某种产品的宣传费,需了解年宣传费x(单位:万元)对年销售收益y(单位:万元)的影响,2016年在若干地区各投入4万元的宣传费,并将各地的销售收益的数据作了初步处理,得到下面的频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.
某公司为确定2017年度投入某种产品的宣传费,需了解年宣传费x(单位:万元)对年销售收益y(单位:万元)的影响,2016年在若干地区各投入4万元的宣传费,并将各地的销售收益的数据作了初步处理,得到下面的频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.| 宣传费x(单位:万元) | 3 | 2 | 1 | 5 | 4 |
| 销售收益y(单位:万元) | 2 | 3 | 2 | 7 | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com