练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    11．数列{an}的前n项和Sn=n2-5n（n∈N*），若p-q=4，则ap-aq=（　　）
    A．20B．16C．12D．8

    分析 根据an=Sn-Sn-1可得an是等差数列，可得答案．

    解答 解：Sn=n2-5n（n∈N*），可得a1=Sn=-4
    当n≥2时，则Sn-1=（n-1）2-5（n-1）=n2+7n+6．
    ∵an=Sn-Sn-1
    ∴an=2n-6，
    当n=1，可得a1=-4
    ∵an-an-1=2常数，∴an是等差数列，首项为-4，公差d=2．
    ∵p-q=4，
    令q=1，则p=5，
    那么a5-a1=8．
    故选D

    点评 本题考查等差的证明与等差数列的性质的运用，考查运算与推理，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    1．甲，乙，丙三个学生数学考试成绩分别为92，75，98．设计一程序计算这三个学生数学成绩的平均分．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．在△ABC中，AB=BC=3，∠BAC=30°，CD是AB边上的高，则$\overrightarrow{CD}•\overrightarrow{CB}$=（　　）
    A．$-\frac{9}{4}$B．$\frac{9}{4}$C．$\frac{27}{4}$D．$-\frac{27}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点分别是F1、F2，离心率为$\frac{1}{2}$，以原点O为圆心，椭圆C的短半轴长为半径的圆与直线x+$\sqrt{2}$y-3=0相切．
    （1）求椭圆C的标准方程；
    （2）动直线l；y=kx+m与椭圆C相切，分别过点F1、F2作直线垂直于l，垂足分别为D、E，求|F1D|+|F2E|的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．下列四个函数中，既是奇函数又在定义域上单调递减的是（　　）
    A．y=2-|x|B．y=tanxC．y=-x3D．$y={log_{\frac{1}{5}}}x$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

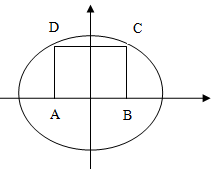    16．如图，长为2$\sqrt{3}$，宽为$\frac{1}{2}$的矩形ABCD，以A、B为焦点的椭圆M：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1恰好过C、D两点．
    （1）求椭圆M的标准方程
    （2）若直线l：y=kx+3与椭圆M相交于P、Q两点，求S△POQ的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．下列说法正确的是（　　）
    A．若x，y∈R，且$\left\{\begin{array}{l}{x+y＞4}\\{xy＞4}\end{array}\right.$，则$\left\{\begin{array}{l}{x＞2}\\{y＞2}\end{array}\right.$
    B．设命题p：?x＞0，x2＞2x，则￢p：?x0≤0，x02≤2${\;}^{{x}_{0}}$
    C．△ABC中，A＞B是sinA＞sinB的充分必要条件
    D．命题“若a=-1，则f（x）=ax2+2x-1只有一个零点”的逆命题为真

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．已知点F1，F2分别是椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的焦点，点B是短轴顶点，直线BF2与椭圆C相交于另一点D．若△F1BD是等腰三角形，则椭圆C的离心率为（　　）
    A．$\frac{1}{3}$B．$\frac{{\sqrt{3}}}{3}$C．$\frac{{\sqrt{2}}}{2}$D．$\frac{{\sqrt{6}}}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．已知点P是函数y=x-2lnx图象上一点，点Q是直线x+y+1=0上的动点，则PQ的最小值为$\frac{3\sqrt{2}}{2}$．

    查看答案和解析>>

    同步练习册答案