练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    6．下列四个函数中，既是奇函数又在定义域上单调递减的是（　　）
    A．y=2-|x|B．y=tanxC．y=-x3D．$y={log_{\frac{1}{5}}}x$

    分析 利用奇偶性、单调性的定义，即可得出结论．

    解答 解：A．y=2-|x|是偶函数；
    B．y=tanx在定义域上不具有单调性；
    C．y=-x3是R上的奇函数且具有单调递减；
    D．y=$lo{g}_{\frac{1}{5}}x$是非奇非偶函数．
    故选：C．

    点评 本题考查了函数的奇偶性、单调性，考查了推理能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    16．计算：
    （Ⅰ）（-$\frac{27}{8}$）${\;}^{-\frac{2}{3}}$+${（0.002）^{-\frac{1}{2}}}$-10（$\sqrt{5}$-2）-1+（$\sqrt{2}$-$\sqrt{3}$）0

    （Ⅱ）$\frac{1}{2}$lg$\frac{32}{49}$-$\frac{4}{3}$lg$\sqrt{8}$+lg$\sqrt{245}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．（1）若直线$\frac{x}{a}+\frac{y}{b}$=1（a＞0，b＞0），过点（1，1），求a+b的最小值．
    （2）已知函数y=$\sqrt{（{m^2}-3m+2）{x^2}+2（m-1）x+5}$的定义域为R，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

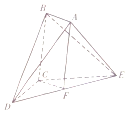    14．在如图所示的多面体ABCDE中，四边形ABCF为平行四边形，F为DE的中点，△BCE为等腰直角三角形，BE为斜边，△BDE为正三角形，CD=CE=2．
    （1）证明：CD⊥BE；
    （2）求四面体ABDE的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．函数$y=\frac{1}{{\sqrt{|x|-x}}}$的定义域为（-∞，0）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．数列{an}的前n项和Sn=n2-5n（n∈N*），若p-q=4，则ap-aq=（　　）
    A．20B．16C．12D．8

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．下列说法正确的是（　　）
    A．若“x=$\frac{π}{4}$，则tanx=1”的逆命题为真命题
    B．在△ABC中，sinA＞sinB的充要条件是A＞B
    C．函数f（x）=sinx+$\frac{4}{sinx}$，x∈（0，π）的最小值为4
    D．?x∈R，使得sinx•cosx=$\frac{3}{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．已知a，b，c分别为△ABC的三个内角A，B，C的对边，c=2，且sin2A+sin2B=sinAsinB+sin2C，则△ABC面积的最大值为（　　）
    A．1B．2C．$\sqrt{3}$D．$2\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．设集合A={m∈Z|m≤-3或m≥2}，B={n∈N|-1≤n＜3}，则B∩（∁ZA）=（　　）
    A．{0，1，2}B．{-1，0，1}C．{0，1}D．{-1，0，1，2}

    查看答案和解析>>

    同步练习册答案