
| A�� | ��x��y��R����$\left\{\begin{array}{l}{x+y��4}\\{xy��4}\end{array}\right.$����$\left\{\begin{array}{l}{x��2}\\{y��2}\end{array}\right.$ | |
| B�� | ������p��?x��0��x2��2x����Vp��?x0��0��x02��2${\;}^{{x}_{0}}$ | |
| C�� | ��ABC�У�A��B��sinA��sinB�ij�ֱ�Ҫ���� | |
| D�� | ���⡰��a=-1����f��x��=ax2+2x-1ֻ��һ����㡱��������Ϊ�� |
���� A����x��y��R����$\left\{\begin{array}{l}{x+y��4}\\{xy��4}\end{array}\right.$����$\left\{\begin{array}{l}{x��2}\\{y��2}\end{array}\right.$�Ǽ����⣬����x=1��y=5��
B��������p��?x��0��x2��2x����Vp��?x0��0��x02��2��
C����ABC��A��B?2RsinA��2RsinB?a��b��
D��f��x��=ax2+2x-1ֻ��һ����㣬⇒a=0��a=-1��
��� �⣺����A����x��y��R����$\left\{\begin{array}{l}{x+y��4}\\{xy��4}\end{array}\right.$����$\left\{\begin{array}{l}{x��2}\\{y��2}\end{array}\right.$�Ǽ����⣬����x=1��y=5���ʴ���
����B��������p��?x��0��x2��2x����Vp��?x0��0��x02��2���ʴ���
����C����ABC�У�A��B?2RsinA��2RsinB?a��b������ȷ��
����D��f��x��=ax2+2x-1ֻ��һ����㣬⇒a=0��a=-1���ʴ���
��ѡ��C
���� ���⿼���˺�������������ٵ��ж��������������ʽ����Ҫ�������ж��������е��⣮


 ͬ��ѧ��һ�ζ���ϵ�д�
ͬ��ѧ��һ�ζ���ϵ�д� �����ܾ�ϵ�д�
�����ܾ�ϵ�д� ���ƿ�����ϵ�д�
���ƿ�����ϵ�д� ���¿쳵����������ϵ�д�
���¿쳵����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | $\frac{2}{3}$ | C�� | $\sqrt{3}$ | D�� | $\frac{{\sqrt{3}}}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
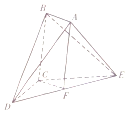 ����ͼ��ʾ�Ķ�����ABCDE�У��ı���ABCFΪƽ���ı��Σ�FΪDE���е㣬��BCEΪ����ֱ�������Σ�BEΪб�ߣ���BDEΪ�������Σ�CD=CE=2��
����ͼ��ʾ�Ķ�����ABCDE�У��ı���ABCFΪƽ���ı��Σ�FΪDE���е㣬��BCEΪ����ֱ�������Σ�BEΪб�ߣ���BDEΪ�������Σ�CD=CE=2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 20 | B�� | 16 | C�� | 12 | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����x=$\frac{��}{4}$����tanx=1���������������� | |
| B�� | �ڡ�ABC�У�sinA��sinB�ij�Ҫ������A��B | |
| C�� | ����f��x��=sinx+$\frac{4}{sinx}$��x�ʣ�0���У�����СֵΪ4 | |
| D�� | ?x��R��ʹ��sinx•cosx=$\frac{3}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | $\sqrt{3}$ | D�� | $2\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��a�Φ���b�Φ�����a��b | B�� | ��a�Φ���b�ͦ����� a��b | ||
| C�� | ��a��b��b�Φ�����a�Φ� | D�� | ��a�ͦ���b�Φ£��� ���ͦ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com