Question

11．已知点P为不等式组$\left\{\begin{array}{l}x-2y+1≥0\\ x≤2\\ x+y-1≥0\end{array}\right.$所表示的平面区域内的一点，点Q是M：（x+1）²+y²=1上的一个动点，则当∠MPQ最大时，|PQ|=（　　）

• A． 1
• B． $\sqrt{2}$
• C． $\frac{{\sqrt{11}}}{3}$
• D． $\frac{{2\sqrt{5}}}{3}$

Answer 1

分析 画出约束条件的可行域，利用图形判断∠MPQ最大时的情况，然后求解PQ的距离

解答 解：不等式组$\left\{\begin{array}{l}x-2y+1≥0\\ x≤2\\ x+y-1≥0\end{array}\right.$表示的可行域如图，由图可知：在△PQM中，MQ=1，当|MP|最短，且PQ与圆相切时，∠MPQ最大，其中${（|{MP}|）_{min}}=\frac{{2\sqrt{5}}}{3}$，此时$|{PQ}|=\sqrt{M{P^2}-1}=\frac{{\sqrt{11}}}{3}$，
故选：C．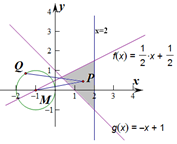

点评 本题考查线性规划的应用，画出可行域以及判断直线与圆的位置关系是解题的关键，考查计算能力．