
| A. | 平行 | B. | 垂直 | C. | 相交但不垂直 | D. | 不能确定 |
分析 对α分类讨论,利用直线相互垂直的充要条件即可判断出位置关系.
解答 解:$α≠\frac{π}{2},\frac{3π}{2}$,0时,直线θ=α与ρcos(θ-α)=1分别化为:y=xtanα,ρcosθcosα+ρsinθsinα=1,化为:xcosα+ysinα=1,其斜率k=$-\frac{1}{tanα}$,由$-\frac{1}{tanα}$×tanα=-1,可知:此时两条直线相互垂直.
α=0,$\frac{π}{2}$,$\frac{3π}{2}$时,两条直线也相互垂直.
因此两条直线的位置关系是相互垂直.
故选:B.
点评 本题考查了极坐标化为直角坐标方程的方法、直线相互垂直的充要条件,考查了分类讨论方法、推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | 8 | C. | 4 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≥3 | B. | a≤-3 | C. | a<-3 | D. | a>3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
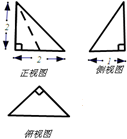
| A. | $\frac{2}{3}$ | B. | $3+\sqrt{2}+\sqrt{3}$ | C. | 2 | D. | $1+2\sqrt{2}+\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p为真 | B. | ¬q为假 | C. | p∧q为真 | D. | p∨q为假 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 11 | B. | 10 | C. | 12 | D. | 13 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com