
���� ��I�������б�ʽ�ó�����=0ʱ��P����=1��=$\frac{5}{216}$��������0ʱ��P����=2��=$\frac{38}{216}$��P����=0��=1-P����=1��-P����=2��=$\frac{173}{216}$�������ʷֲ����⣮
��II�����÷ֲ��еó��������ѧ�������ҵ������ѧ�������жϼ��ɣ�
��� ���⣺�εĿ���ȡֵΪ0��1��2��f��x��=ax2+bx+c���б�ʽ��=b2-4ac��
����=0ʱ��bΪż����b=2ʱ��a=1��c=1��
b=4ʱ��a=1��c=4��a=2��c=2��a=4��c=1��
b=6ʱ��a=3��c=3��
��P����=1��=$\frac{5}{216}$��
��b��3��b=3ʱ��ac��2����3�֣�
b=4ʱ��ac��4����9�֣�b=5ʱ��ac��6��
��14�֣�b=6ʱ��ac��9����17�֣�����43�֣�
���=1��������43-5=38�֣�
��P����=2��=$\frac{38}{216}$��
P����=0��=1-P����=1��-P����=2��=$\frac{173}{216}$��
��εķֲ���Ϊ��
| �� | 0 | 1 | 2 |
| P | $\frac{173}{216}$ | $\frac{5}{216}$ | $\frac{38}{216}$ |
���� ���⿼��ŵ�����ʵ����ŵ������ʵ��������Ӧ�ã���Ϻ����������жϸ��ʵ������𣬷�������ƽ���Ҫ�������Ƿ���ȣ������е���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2014}$ | B�� | $\frac{1}{{2}^{2014}}$ | C�� | $\frac{1}{2015}$ | D�� | $\frac{1}{{2}^{2015}}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{6}$ | B�� | $2\sqrt{3}$ | C�� | 2 | D�� | $\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
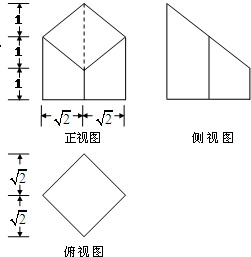 ij�������屻һ��ƽ�����أ��õ��ļ����������ͼ��ͼ��ʾ��������������ȫ���Ϊ20+2$\sqrt{6}$��ƽ����λ����
ij�������屻һ��ƽ�����أ��õ��ļ����������ͼ��ͼ��ʾ��������������ȫ���Ϊ20+2$\sqrt{6}$��ƽ����λ�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com