
【题目】四棱锥A-BCDE中,侧棱AD⊥底面BCDE,底面BCDE是直角梯形,DE∥BC,BC⊥CD,BC=2AD=2DC=2DE=4,H,I分别是AD,AE的中点.

(Ⅰ)在AB上求作一点F,BC上求作一点G,使得平面FGI∥平面ACD;
(Ⅱ)求平面CHI将四棱锥A-BCDE分成的两部分的体积比.
【答案】(Ⅰ)见解析(Ⅱ) ![]() .
.
【解析】试题分析:(Ⅰ)通过证明 IG∥HC和FG∥AC.从而平面FGI∥平面ACD.
(Ⅱ)先求得四棱锥A-BCHI的体积V1=![]() ×
×![]() ×
×![]() =
=![]() ,和四棱锥A-BCDE的体积V=
,和四棱锥A-BCDE的体积V=![]() ×
×![]() ×(2+4)×2×2=4,通过作差得到多面体HI-ABCD的体积V2=V-V1=
×(2+4)×2×2=4,通过作差得到多面体HI-ABCD的体积V2=V-V1=![]() ,可得两部分体积比为
,可得两部分体积比为![]() .
.
试题解析:(Ⅰ)如右图所示,分别作AB的四等分点F(离A较近),BC的四等分点G(离C较近),则其使得平面FGI∥平面ACD.
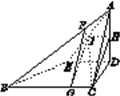
证明如下:
因为H,I分别是AD,AE的中点,
所以HI∥DE,
且HI=![]() DE.
DE.
又DE∥BC,BC=2DE,
所以HI∥BC且HI=![]() BC.
BC.
所以HI∥GC且HI=GC.
所以四边形HIGC是平行四边形.
所以IG∥HC.
由题意, ![]() ,所以FG∥AC.
,所以FG∥AC.
又IG∩FG=G,HC∩AC=C,所以平面FGI∥平面ACD.
(Ⅱ)连接BI,∵H,I分别为AD,AE中点,∴HI∥DE,HI=![]() DE=1,
DE=1,

又DE∥BC,∴HI∥BC,
∴平面CHI将四棱锥分成四棱锥A-BCHI与多面体HI-ABCD两部分,
过D作DM⊥CH,垂足为M,则A到平面BCHI的距离等于DM,
∵AD⊥平面BCDE,∴AD⊥CD,
在Rt△CDH中,CD=2,DH=1,
CH=![]() ,DM=
,DM=![]() ,
,
∵BC⊥CD,AD⊥BC,AD∩CD=D,
∴BC⊥平面ACD,
∵CH平面ACD,∴BC⊥CH,
四边形BCHI的面积为![]() (1+4)×
(1+4)×![]() =
=![]() ,
,
四棱锥A-BCHI的体积V1=![]() ×
×![]() ×
×![]() =
=![]() ,
,
四棱锥A-BCDE的体积V=![]() ×
×![]() ×(2+4)×2×2=4,
×(2+4)×2×2=4,
多面体HI-ABCD的体积V2=V-V1=![]() ,
,
∴平面CHI将四棱锥A-BCDE分成的两部分体积比为![]() .
.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的前n项和为Sn,且满足Sn=2n+1+2p(n∈N*).
(1)求p的值及数列{an}的通项公式;
(2)若数列{bn}满足![]() =(3+p)anbn,求数列{bn}的前n项和Tn.
=(3+p)anbn,求数列{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2018·日照一模)如图所示,ABCD-A1B1C1D1是长方体,O是B1D1的中点,直线A1C交平面AB1D1于点M,给出下列结论:

①A、M、O三点共线;②A、M、O、A1不共面;③A、M、C、O共面;④B、B1、O、M共面.
其中正确结论的序号为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)的定义域为D,如果x∈D,y∈D,使得f(x)=-f(y)成立,则称函数f(x)为“Ω函数”.给出下列四个函数:①y=sin x;②y=2x;③y=![]() ;④f(x)=ln x.则其中“Ω函数”共有( )
;④f(x)=ln x.则其中“Ω函数”共有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是等差数列,a10=4a3,a4=3a1+7.
(1)求通项公式an;
(2)若bn=an-2an+2,求数列{bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正项等差数列{an}满足a1=4,且a2,a4+2,2a7-8成等比数列,{an}的前n项和为Sn.
(1)求数列{an}的通项公式;
(2)令![]() ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() (a∈R).
(a∈R).
(Ⅰ)求f(x)的单调区间与极值;
(Ⅱ)若函数f(x)的图象与函数g(x)=1的图象在区间(0,e2]上有两个公共点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856264)
已知函数f(x)=aln x,e为自然对数的底数.
(Ⅰ)曲线f(x)在点A(1,f(1))处的切线与坐标轴所围成的三角形的面积为2,求实数a的值;
(Ⅱ)若f(x)≥1-![]() 恒成立,求实数a的值取值范围.
恒成立,求实数a的值取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com