
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 以上都有可能 |
分析 可将l1的方程整理为(x+2)m+(-x-y+1)=0,利用$\left\{\begin{array}{l}{x+2=0}\\{-x-y+1=0}\end{array}\right.$,可确定直线l过定点为圆心,即可得出结论.
解答 解:将l1的方程整理为(x+2)m+(-x-y+1)=0,
由$\left\{\begin{array}{l}{x+2=0}\\{-x-y+1=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-2}\\{y=3}\end{array}\right.$,
∴直线l过定点(-2,3)即圆心,
∴直线l1恒与圆有两个交点,
故选:A.
点评 本题考查直线系方程的应用,考查直线与圆的位置关系,考查转化思想,确定直线l过定点.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示:四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,给出下列结论:
如图所示:四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,给出下列结论:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
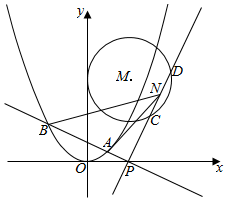 如图,抛物线E:x2=2py(p>0)的焦点为$(0,\frac{1}{4})$,圆心M在射线y=2x(x≥0)上且半径为1的圆M与y轴相切.
如图,抛物线E:x2=2py(p>0)的焦点为$(0,\frac{1}{4})$,圆心M在射线y=2x(x≥0)上且半径为1的圆M与y轴相切.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com