
分析 (1)求出函数的导数,通过讨论m的范围,求出函数的单调区间,从而求出函数f(x)在闭区间上的最小值即可;
(2)根据f(x)的单调性,通过讨论n的符号,解关于f(x)的不等式结合不等式解的个数,求出n的范围即可.
解答 解:(1)f′(x)=$\frac{1-ln(\sqrt{3}x)}{{x}^{2}}$,令f′(x)>0,得f(x)的递增区间为(0,$\frac{\sqrt{3}}{3}$e);
令f′(x)<0,得f(x)的递减区间为($\frac{\sqrt{3}}{3}$e,+∞),…(2分)
∵x∈[1,m],则当1≤m≤$\frac{\sqrt{3}}{3}$e时,f(x)在[1,m]上为增函数,
f(x)的最小值为f(1)=$\frac{ln3}{2}$;
当m>$\frac{\sqrt{3}}{3}$e时,f(x)在[1,$\frac{\sqrt{3}}{3}$e)上为增函数,
在($\frac{\sqrt{3}}{3}$e,m]上为减函数,又f(3)=$\frac{ln3}{2}$=f(1),
∴若$\frac{\sqrt{3}}{3}$e<m≤3,f(x)的最小值为f(1)=$\frac{ln3}{2}$,…(4分)
若m>3,f(x)的最小值为f(m)=$\frac{ln(\sqrt{3}m)}{m}$,
综上,当1≤m≤3时,f(x)的最小值为f(1)=$\frac{ln3}{2}$;
当m>3,f(x)的最小值为f(m)=$\frac{ln(\sqrt{3}m)}{m}$…(6分)
(2)由(1)知,f(x)的递增区间为(0,$\frac{\sqrt{3}}{3}$e),递减区间为($\frac{\sqrt{3}}{3}$e,+∞),
且在($\frac{\sqrt{3}}{3}$e,+∞)上,ln$\sqrt{3}$x>lne=1>0,又x>0,则f(x)>0,又f($\frac{\sqrt{3}}{3}$)=0,
∴n<0时,由不等式f2(x)-nf(x)>0得f(x)>0或f(x)<n,
而f(x)>0的解集为($\frac{\sqrt{3}}{3}$,+∞),整数解有无数多个,不合题意;…(8分)
n=0时,由不等式f2(x)-nf(x)>0,得f(x)≠0,解集为(0,$\frac{\sqrt{3}}{3}$)∪($\frac{\sqrt{3}}{3}$,+∞),
整数解有无数多个,不合题意;…(10分)
n>0时,由不等式f2(x)-nf(x)>0,得f(x)>n或f(x)<0,
∵f(x)<0的解集为(0,$\frac{\sqrt{3}}{3}$)无整数解,
若不等式f2(x)-nf(x)>0有且只有三个整数解,
∵f(x)在(0,$\frac{\sqrt{3}}{3}$e)递增,在($\frac{\sqrt{3}}{3}$e,+∞)递减,
而1<$\frac{\sqrt{3}}{3}$e<2,f(1)=f(3),
所以,三个正整数为1,2,3,而f(4)=$\frac{ln4\sqrt{3}}{4}$,
综上,实数n的取值范围是[$\frac{ln4\sqrt{3}}{4}$,$\frac{ln3}{2}$)…(12分)
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,转化思想,是一道综合题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m<3 | B. | m≤3 | C. | m≤-3 | D. | m<-3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {y|0$<y<\frac{1}{2}$} | B. | ∅ | C. | {y|$\frac{1}{2}$<y<1} | D. | {y|0<y<1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①③ | B. | ②③ | C. | ①②④ | D. | ①③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 11或12 | C. | 12 | D. | 12或13 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
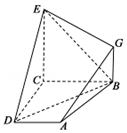 如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE=$\frac{π}{2}$,平面ABCD⊥平面BCEG,BC=CD=CE=2,AD=BG=1.
如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE=$\frac{π}{2}$,平面ABCD⊥平面BCEG,BC=CD=CE=2,AD=BG=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
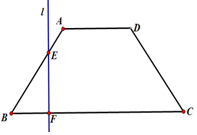 如图,已知底角为45°的等腰梯形ABCD,底边BC长为12,腰长为4$\sqrt{2}$,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分.
如图,已知底角为45°的等腰梯形ABCD,底边BC长为12,腰长为4$\sqrt{2}$,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com