
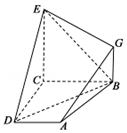
 如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE=$\frac{π}{2}$,平面ABCD⊥平面BCEG,BC=CD=CE=2,AD=BG=1.
如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE=$\frac{π}{2}$,平面ABCD⊥平面BCEG,BC=CD=CE=2,AD=BG=1.分析 (1)取BE中点H,连结DH,则可证四边形ADHG为平行四边形,从而得到AG∥DH,推出AG∥平面BDE;
(2)由题意建立如图所示空间直角坐标系,结合已知求出所用点的坐标,进一步求得$\overrightarrow{AB}$及平面BDE的一个法向量,由两向量所成角的余弦值可得AB与平面BDE所成角的正弦值.
解答 (1)证明:过G作GF⊥CE交BE于H,连结DH,则四边形BCFG是矩形,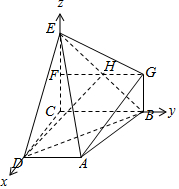
∴CF=BG,则F是CE的中点,H是FG的中点,
∴HG=$\frac{1}{2}$BC,HG∥BC,
∵AD∥BC,AD=$\frac{1}{2}$BC,
∴AD=HG,AD∥HG,则四边形ADHG是平行四边形,
∴AG∥DH,
∵DH?平面BDE,AG?平面BDE,
∴AG∥平面BDE;
(2)解:由题意建立如图所示空间直角坐标系,
∵BC=CD=CE=2,AD=BG=1,
∴D(2,0,0),B(0,2,0),E(0,0,2),A(2,1,0),
则$\overrightarrow{AB}=(-2,1,0)$,$\overrightarrow{DB}=(-2,2,0),\overrightarrow{DE}=(-2,0,2)$,
设平面BDE的一个法向量为$\overrightarrow{m}=(x,y,z)$,
由$\left\{\begin{array}{l}{\overrightarrow{DB}•\overrightarrow{m}=-2x+2y=0}\\{\overrightarrow{DE}•\overrightarrow{m}=-2x+2z=0}\end{array}\right.$,取z=1,得$\overrightarrow{m}=(1,1,1)$,
∴AB与平面BDE所成角的正弦值sinθ=|$\frac{\overrightarrow{AB}•\overrightarrow{m}}{|\overrightarrow{AB}||\overrightarrow{m}|}$|=|$\frac{-2×1+1×1}{\sqrt{(-2)^{2}+{1}^{2}}×\sqrt{3}}$|=$\frac{\sqrt{15}}{15}$.
点评 本题考查直线与平面平行的判定,训练了利用空间向量求线面角,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 高中 | 本科 | 硕士 | 博士 | 合计 | |
| 35岁以下 | 10 | 150 | 50 | 35 | 245 |
| 35~50岁 | 20 | 100 | 20 | 13 | 153 |
| 50岁以上 | 30 | 60 | 10 | 2 | 102 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,5] | B. | [10,+∞) | C. | (-∞,5]∪[10,+∞) | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,$\sqrt{2}$+1) | B. | ($\sqrt{2}$,$\sqrt{2}$+1) | C. | ($\sqrt{2}$,2) | D. | ($\sqrt{2}$,2)∪(2,$\sqrt{2}$+1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | 1 | C. | $\frac{\sqrt{5}}{2}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com